袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求取球两次终止的概率
(3)求甲取到白球的概率
(本小题满分14分)已知抛物线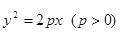 ,焦点为
,焦点为 ,一直线
,一直线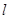 与抛物线交于
与抛物线交于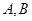 两点,且
两点,且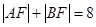 ,
,
(1)求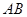 的中点的横坐标
的中点的横坐标
(2)若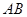 的垂直平分线恒过定点
的垂直平分线恒过定点 求抛物线的方程;
求抛物线的方程;
(3)求在条件(2)下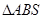 面积的最大值.
面积的最大值.
(本小题满分14分)
已知数列 的前
的前 项和
项和 ,函数
,函数 对
对 有
有 ,数列
,数列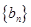 满足
满足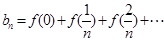
 .
.
(1)分别求数列 、
、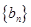 的通项公式;
的通项公式;
(2)若数列 满足
满足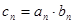 ,
,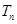 是数列
是数列 的前
的前 项和,若存在正实数
项和,若存在正实数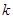 ,使不等式
,使不等式 对于一切的
对于一切的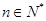 恒成立,求
恒成立,求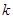 的取值范围.
的取值范围.
(本小题满分14分)已知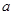 为实数,
为实数,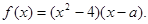
(1)若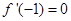 ,求
,求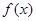 在
在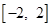 上最大值和最小值;
上最大值和最小值;
(2)若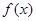 在
在 和
和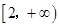 上都是递增的,求
上都是递增的,求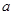 的取值范围。
的取值范围。
(本小题满分14分)如图,已知矩形 中,
中,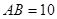 ,
,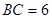 ,将矩形沿对角线
,将矩形沿对角线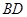 把△
把△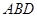 折起,使
折起,使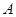 移到
移到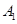 点,且
点,且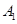 在平面
在平面 上的射影
上的射影 恰好在
恰好在 上.
上.
(1)求证: ;
;
(2)求证:平面 平面
平面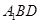 ;
;
(3)求三棱锥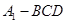 的体积.
的体积.
(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,且经过定点
,且经过定点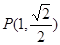

(1)求椭圆 的方程;
的方程;
(2)设直线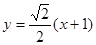 交椭圆
交椭圆 于
于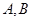 两点,求线段
两点,求线段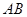 的长.
的长.