已知离心率为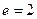 的双曲线
的双曲线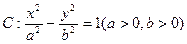 ,双曲线
,双曲线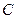 的一个焦点到
的一个焦点到
渐近线的距离是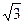
(1)求双曲线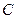 的方程
的方程
(2)过点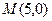 的
的 直线
直线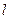 与双曲线
与双曲线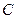 交于
交于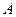 、
、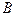 两点,交
两点,交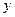 轴于
轴于 点
点 ,当
,当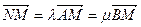 ,且
,且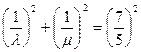 时,求直线
时,求直线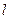 的方程
的方程
角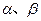 (
(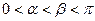 )的终边与单位圆分别交于A、B两点,已知A、B的横坐标分别为
)的终边与单位圆分别交于A、B两点,已知A、B的横坐标分别为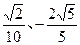 .试求:
.试求:
(Ⅰ)tan(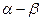 );
);
(Ⅱ)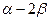 .
.
已知平面向量a=(1,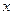 ),b=(2
),b=(2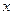 +3,-
+3,-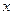 )(
)(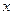 ∈R).
∈R).
(Ⅰ)若a⊥b,求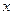 的值;
的值;
(Ⅱ)若a∥ b,求|a-b|.
已知函数 .
.
(Ⅰ)求函数 的最小正周期及图象的对称轴方程;
的最小正周期及图象的对称轴方程;
(Ⅱ)设函数 ,求
,求 的值域.
的值域.
(本小题满分16分)
已知 为实数,函数
为实数,函数 ,函数
,函数 ,
,
令函数 .
.
⑴若 ,求函数
,求函数 的极小值;
的极小值;
⑵当 时,解不等式
时,解不等式 ;
;
⑶当 时,求函数
时,求函数 的单调区间.
的单调区间.
(本小题满分16分)
已知数列 满足
满足 ,当
,当 ,
, 时,
时, .
.
⑴求数列 的通项公式;
的通项公式;
⑵是否存在 ,使得
,使得 时,不等式
时,不等式 对任意实数
对任意实数 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
⑶在 轴上是否存在定点
轴上是否存在定点 ,使得三点
,使得三点 、
、 、
、 (其中
(其中 、
、 、
、 是互不相等的正整数且
是互不相等的正整数且 )到定点
)到定点 的距离相等?若存在,求出点
的距离相等?若存在,求出点 及正整数
及正整数 、
、 、
、 ;若不存在,说明理由.
;若不存在,说明理由.