(本小题12分)已知三次函数 的导函数
的导函数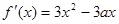 ,
, ,(
,( ,
,
 ).
).
(1)若曲线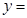
 在点(
在点(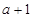 ,
, )处切线的斜率为12,求
)处切线的斜率为12,求 的值;
的值;
(2)若 在区间[-1,1]上的最小值,最大值分别为-2和1,且
在区间[-1,1]上的最小值,最大值分别为-2和1,且 ,求函数
,求函数 的解析式.
的解析式.
在平面直角坐标系 中,已知直线
中,已知直线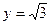 被圆[
被圆[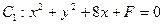 截得的弦长为
截得的弦长为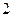
(Ⅰ)求圆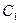 的方程
的方程
(II)设圆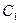 和
和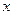 轴相交于
轴相交于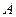 ,
, 两点,点
两点,点 为圆
为圆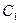 上不同于
上不同于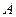 ,
, 的任意一点,直线
的任意一点,直线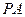 ,
,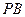 交
交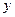 轴于
轴于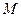 ,
, 两点.当点
两点.当点 变化时,以
变化时,以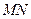 为直径的圆
为直径的圆 是否经过圆
是否经过圆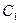 内一定点?请证明你的结论
内一定点?请证明你的结论
已知圆C过点(4,-1),且与直线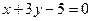 相切于点
相切于点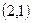 .
.
(Ⅰ)求圆C的方程;
(II)是否存在斜率为1的直线l,使得l被圆C截得弦AB,以AB为直径的圆经过原点,若存在,求出直线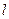 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知圆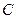 以
以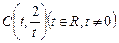 为圆心且经过原点O,与
为圆心且经过原点O,与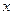 轴交于另一点A,与
轴交于另一点A,与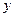 轴交于另一点B.
轴交于另一点B.
(Ⅰ)求证: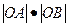 为定值
为定值
(Ⅱ) 若直线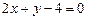 与圆
与圆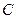 交于点
交于点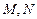 ,若
,若 ,求圆
,求圆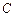 的方程.
的方程.
本题满分10分)如图,在长方体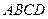 -
-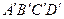 中,
中,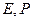 分别是
分别是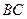 ,
, 的中点,
的中点, 分别是
分别是 ,
, 中点,
中点,

(Ⅰ)求三棱锥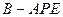 的体积;
的体积;
(Ⅱ)求证: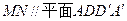
已知直线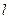 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线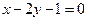 .
.
(Ⅰ)求直线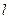 的方程;
的方程;
(Ⅱ)求直线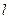 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积 .
.