(文科)已知中心在原点,焦点在x轴上的椭圆的离心率为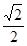 ,
, 为其焦点,一直线过点
为其焦点,一直线过点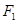 与椭圆相交于
与椭圆相交于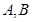 两点,且
两点,且 的最大面积为
的最大面积为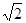 ,求椭圆的方程。
,求椭圆的方程。
如图,在三棱锥 中,平面 平面 , , 为 的中点.
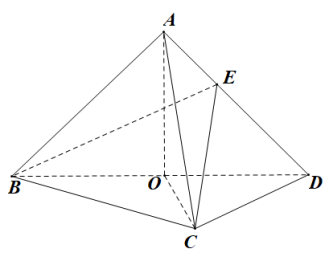
(1)证明: ;
(2)若 是边长为1的等边三角形,点 在棱 上, ,且二面角 的大小为 ,求三棱锥 的体积.
记 是内角 , , 的对边分别为 , , .已知 ,点 在边 上, .
(1)证明: ;
;
(2)若
,求
某学校组织“一带一路”知识竞赛,有A,B两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束:若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分:B类问题中的每个问题回答正确得80分,否则得0分,己知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记 为小明的累计得分,求 的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
已知数列 满足 ,
(1)记 ,写出 , ,并求数列 的通项公式;
(2)求 的前20项和.
已知函数 .
(1)当 时,求不等式 的解集;
(2)若 ,求 a的取值范围.