平面直角坐标系中有一个△ABC,角A,B,C所对应的边分别为 ,已知坐标原点与顶点B重合,且
,已知坐标原点与顶点B重合,且 ,
,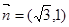 ,
,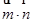 =
=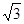 ,且∠A为锐角。
,且∠A为锐角。
(1)求角A的大小;
(2)若 ,求实数
,求实数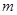 的取值范围;
的取值范围;
(3)若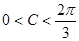 ,顶点A
,顶点A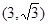 ,
, ,求△ABC的面积。
,求△ABC的面积。
在平面直角坐标系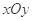 中,点
中,点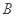 与点
与点 关于原点
关于原点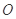 对称,
对称,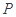 是动点,且直线
是动点,且直线 与
与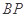 的斜率之积等于
的斜率之积等于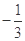 .
.
(1)求动点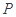 的轨迹方程;
的轨迹方程;
(2)设直线 和
和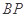 分别与直线
分别与直线 交于点
交于点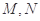 ,问:是否存在点
,问:是否存在点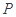 使得
使得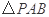 与
与 的面积相等?若存在,求出点
的面积相等?若存在,求出点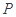 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
在一次考试中,5名同学数学、物理成绩如下表所示:
| 学生 |
A |
B |
C |
D |
E |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)根据表中数据,求物理分 对数学分
对数学分 的回归方程:
的回归方程:
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以 表示选中的同学中物理成绩高于90分的人数,求随机变量
表示选中的同学中物理成绩高于90分的人数,求随机变量 的分布列及数学期望
的分布列及数学期望 .(附:回归方程
.(附:回归方程 中,
中, ,
, )
)
如图,在三棱柱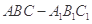 中,已知
中,已知 ,
,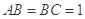 ,
,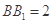 ,
,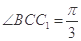 .
.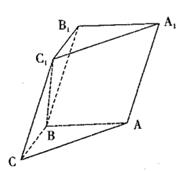
(1)求证: ;
;
(2)设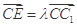 (
( ),且平面
),且平面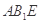 与
与 所成的锐二面角的大小为30°,试求的值.
所成的锐二面角的大小为30°,试求的值.
已知数列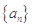 满足
满足 ,
, ,
,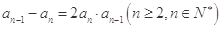 .
.
(1)求证: 是等差数列;
是等差数列;
(2)证明: .
.
已知向量 ,
,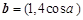 ,
,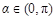 .
.
(1)若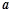 ⊥
⊥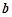 ,求
,求 的值;
的值;
(2)若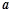 ∥
∥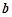 ,求
,求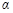 的值.
的值.