已知 是复数,
是复数,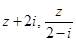 均为实数,
均为实数,
(1)求复数 ;
;
(2)若复数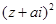 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数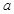 的取值范围.
的取值范围.
(本小题满分14分)已知数列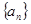 中,
中,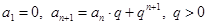 ,
,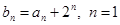 ,2,3,…
,2,3,…
(Ⅰ)求证数列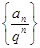 是等差数列;
是等差数列;
(Ⅱ)试比较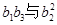 的大小;
的大小;
(Ⅲ)求正整数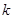 ,使得对于任意的正整数
,使得对于任意的正整数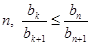 恒成立.
恒成立.
(本小题满分14分)设函数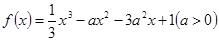 .
.
(Ⅰ)求函数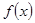 的单调区间、极大值和极小值.
的单调区间、极大值和极小值.
(Ⅱ)若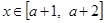 时,恒有
时,恒有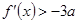 ,求实数
,求实数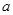 的取值范围.
的取值范围.
(本小题满分13分)已知等差数列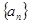 的前
的前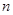 项和为
项和为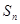 ,已知
,已知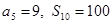 .
.
(Ⅰ)求通项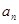 ;
;
(Ⅱ)记数列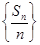 的前
的前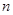 项和为
项和为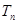 ,数列
,数列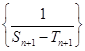 的前
的前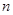 项和为
项和为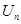 ,求证:
,求证: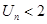 .
.
(本小题满分13分)如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为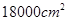 四周空白的宽度为
四周空白的宽度为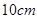 ,两栏之间的中缝空白宽度为
,两栏之间的中缝空白宽度为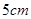 ,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?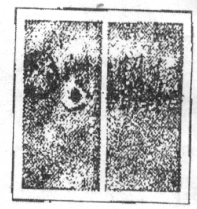
(本小题满分13分)已知函数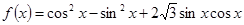 .
.
(Ⅰ)求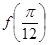 的值和函数
的值和函数 的最小正周期;
的最小正周期;
(Ⅱ)求 的单调递减区间及最大值,并指出相应的
的单调递减区间及最大值,并指出相应的 的取值集合.
的取值集合.