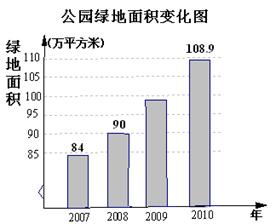
某新建公园的绿化给公园自身及周边的环境都带来了明显的改变，下面的条形图是这个新建公园近几年来绿地面积的变化图，请你根据图中所给的数据解答下列问题：求这个公园2008年底至2010年底这两年绿地面积的年平均增长率；
如果这个平均增长率保持不变，请你预测2011年底这个公园的绿地面积将达到多少万平方米？
把大小和形状完全相同的6张卡片分成两组，每组3张，分别标上数字1、2、3，将这两组卡片分别放入两个盒子中搅匀，再从中各随机投取一张．
（1）试求取出的两张卡片数字之和为奇数概率；
（2）若取出的两张卡片数字之和为奇数，则甲胜；取出的两张卡片数字之和为偶数，则乙胜；试分析这个游戏是否公平？请说明理由．
如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连接EF与边CD相交于点G，连接BE与对角线AC相交于点H, AE=CF，BE=EG。
(1)求证：EF//AC;
(2)求∠BEF大小；
(3)求证：
如图，点A是反比例函数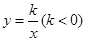
上一点，作AB⊥x轴于点B，且△AOB的面积为2，点A坐标为(-1，m)。
(1)求k和m的值。
(2)若直线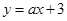
经过点A，交另一支双曲线于点C，求△AOC的面积。
(3)指出x取何值时，一次函数的值大于反比例函数的值，直接写出结果。
(4)在y轴上是否存在点P，使得△PAC的面积为6，如果存在，请求出点P的坐标；若不存在，请说明理由．
如图，在△AFC中，AF=AC，B是CF的中点，AH平分∠CAF，作CD⊥AH于D。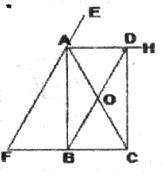
(1)证明四边形ABCD是矩形。
(2)若BD交AC于O，证明：OB//AF且OB= 
AF。
(3)若使四边形ABCD是正方形，需添加一个条件，请直接写出该条件。
如图，在等腰梯形ABCD中，AD//BC，AD="3" cm，BC="7" cm，∠B=60°，P为下底BC上一点（不与B、C重合），连接AP，过P点作PE交DC于E，使得∠APE=∠B.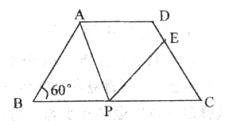
(1)求证：△ABP∽△PCE;
(2)求等腰梯形的腰AB的长；
(3)在底边BC上是否存在一点P，使得DE:EC=5:3？如果存在，求出BP的长，如果不存在，请说明理由．