新浪网作了一次民意调查，当问及消费者“认为我们国家今年的经济状况怎么样？”时，调查结果显示：42.4%的消费者认为今年我国经济保持平稳，16.7%的消费者认为经济将逐渐繁荣，33.1%的消费者认为将出现经济放缓或下行，部分消费者回答“不清楚”。见图。请回答下列问题：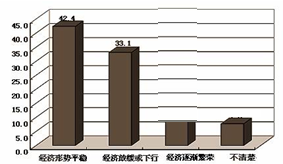
图中“经济将逐渐繁荣”这一组的柱状图画得不完整，请补全。
回答“不清楚”的消费者所占比例为 。其中“42.4%、16.7%”等在统计学中叫 。
回答“经济放缓或下行”的人数为0.662万人，那么认为“经济将逐渐繁荣”的人数是 万人。
虽然，消费者对我国今年经济形势的判断存在一定的分歧，但多数仍持相对乐观态度，认为经济形势平稳或者逐步繁荣的被访者占到了近 成（注：一成=10%）。
（1）计算：|
﹣2|﹣
×tan60°+2cos30°+（
）﹣1
（2）解方程：2x2﹣5x+1=0．
如图，抛物线y=ax2+bx+3经过A（﹣1，0），B（3，0）两点，且交y轴于点C，对称轴与抛物线相交于点P、与直线BC相交于点M．
（1）求该抛物线的解析式．
（2）在抛物线上是否存在一点N，使得|MN﹣ON|的值最大？若存在，请求出点N的坐标；若不存在，请说明理由．
（3）连接PB，请探究：在抛物线上是否存在一点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．
如图，已知☉O的直径AB=8，过A、B两点作☉O的切线AD、BC．
（1）当AD=2，BC=8时，连接OC、OD、CD．
①求△COD的面积．
②试判断直线CD与☉O的位置关系，并说明理由．
（2）若直线CD与☉O相切于点E，设AD=x（x＞0），试用含x的式子表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．
为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？
在Rt△ABC中，∠ACB=90°，现将Rt△ABC绕点C逆时针旋转90°，得到Rt△DEC（如图①）
（1）请判断ED与AB的位置关系，并说明理由．
（2）如图②，将Rt△DEC沿CB方向向右平移，且使点D恰好落在AB边上，记平移后的三角形为Rt△DEF，连接AE、DC，求证：∠ACD=∠AED．