金银花自古被誉为清热解毒的良药，同时也是很多高级饮料的常用原料．“渝蕾一号”为重庆市中药研究院所选育的金银花优良品种，较传统金银花具有质量好、产量高、结蕾整齐等优点．某花农于前年引进一批“渝蕾一号”金银花种苗进行种植，去年第一次收获．因金银花入药或作饮料需要使用干燥花蕾，该花农将收获的新鲜金银花全部干燥成干花蕾后出售．根据经验，每亩鲜花蕾产量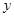
（千克）与每亩种苗数
（株）满足关系式：
，每亩成本
（元）与每亩种苗数（株）之间的函数关系满足下表：
| 每亩种苗数（株） |
100 |
110 |
120 |
130 |
140 |
| 每亩成本（元） |
1800 |
1860 |
1920 |
1980 |
2040 |
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求出与的函数关系式；
（2）若该品种金银花的折干率为20%（即每100千克鲜花蕾，干燥后可得20千克干花蕾），去年每千克干花蕾售价为200元，则当每亩种苗数为多少时，每亩销售利润
可获得最大值，并求出该最大利润；（利润=收入
成本）
（3）若该花农按照（2）中获得最大利润的方案种植，并不断改善种植技术，今年每亩鲜花蕾产量比去年增加
%．但由于市场上同类产品数量猛增，造成每千克干花蕾的售价比去年降低
%，结果今年每亩销售总额为45810元．请你参考以下数据，估算出
的整数值（
）．
（参考数据：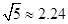
，
，
，
）
在平面直角坐标系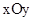
中，抛物线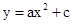
与x轴交于点A（-2,0）和点B，与y轴交于点C（0,
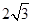），线段AC上有一动点P从点A出发，以每秒1个单位长度的速度向点C移动，线段AB上有另一个动点Q从点B出发，以每秒2个单位长度的速度向点A移动，两动点同时出发，设运动时间为t秒.
（1）求该抛物线的解析式；
（2）在整个运动过程中，是否存在某一时刻，使得以A，P，Q为顶点的三角形与△AOC相似?如果存在，请求出对应的t的值;如果不存在，请说明理由.
（3）在y轴上有两点M（0，m）和N（0，m+1），若要使得AM+MN+NP的和最小，请直接写出相应的m、t的值以及AM+MN+NP的最小值.
在等腰直角△ABC中，∠BAC=90°，AB=AC，
（1）如图1，点D、E分别是AB、AC边的中点，AF⊥BE交BC于点F，连结EF、CD交于点H.求证，EF⊥CD；
（2）如图2，AD=AE，AF⊥BE于点G交BC于点F，过F作FP⊥CD交BE的延长线于点P，试探究线段BP,FP,AF之间的数量关系，并说明理由.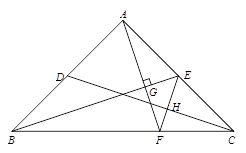
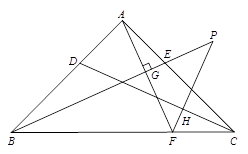
图1图2
已知二次函数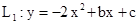
与x轴交于A（1,0）、B（3,0）两点；二次函数
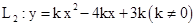的顶点为P.
（1）请直接写出：b=_______，c=___________；
（2）当∠APB=90°，求实数k的值;
（3）若直线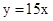
与抛物线L2交于E，F两点，问线段EF的长度是否发生变化？如果不发生变化，请求出EF的长度；如果发生变化，请说明理由.
在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分？他画出了如下示意图（如图1），得到了符合要求的直线AF.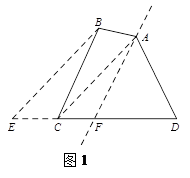
小明的作图步骤如下：
第一步：连结AC；
第二步：过点B作BE//AC交DC的延长线于点E；
第三步：取ED中点F，作直线AF；
则直线AF即为所求.
请参考小明思考问题的方法，解决问题：
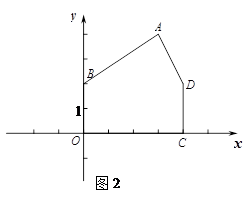
如图2，五边形ABOCD，各顶点坐标为：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).请你构造一条经过顶点A的直线，将五边形ABOCD分为面积相等的两部分，并求出该直线的解析式.
为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：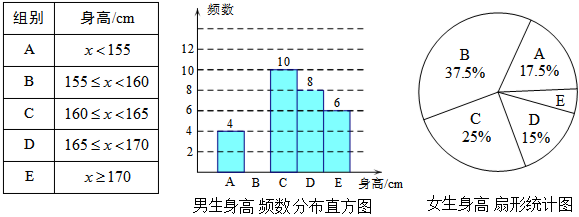
根据图表提供的信息，回答下列问题：
（1）样本中，女生身高在E组的有2人，抽样调查了__________名女生，共抽样调查了__________名学生；
(2) 补全条形统计图；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x <170之间的学生约有多少人.