有三块牧场,草长得一样密一样快,面积分别为 公顷,10公顷和24公顷,第一块12头牛可吃4星期,第二块21头牛可吃9星期,第三块可供多少头牛吃18个星期?
公顷,10公顷和24公顷,第一块12头牛可吃4星期,第二块21头牛可吃9星期,第三块可供多少头牛吃18个星期?
在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y=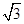 x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y= (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=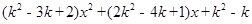 (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
如图,在直角坐标系中,⊙M经过原点O(0,0),点A(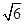 ,0)与点B(0,-
,0)与点B(0,-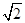 ),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。
),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。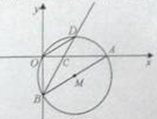
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标。
现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件。现假定该公司每月的投递总件数的增长率相同:
(1)求该快递公司投递快递总件数的月平均增长率;
(2)如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F。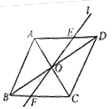
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度。
中华文明,源远流长:中华汉字,寓意深广。为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分。为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表: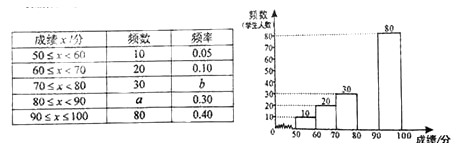
请根据所给的信息,解答下列问题:
(1)a=,b=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人?