现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件。现假定该公司每月的投递总件数的增长率相同:
(1)求该快递公司投递快递总件数的月平均增长率;
(2)如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
佳佳文具店购进 , 两种款式的笔袋,其中 种笔袋的单价比 种袋的单价低 .已知店主购进 种笔袋用了810元,购进 种笔袋用了600元,且所购进的 种笔袋的数量比 种笔袋多20个.请问:文具店购进 , 两种款式的笔袋各多少个?
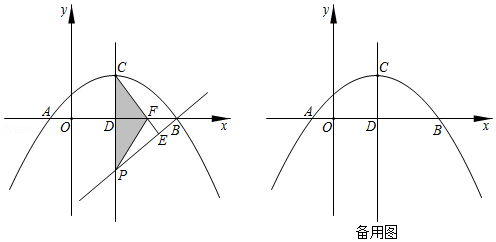
抛物线 与 轴交于 , 两点,顶点为 ,对称轴交 轴于点 ,点 为抛物线对称轴 上的一动点(点 不与 , 重合).过点 作直线 的垂线交 于点 ,交 轴于点 .
(1)求抛物线的解析式;
(2)当 的面积为5时,求点 的坐标;
(3)当 为等腰三角形时,请直接写出点 的坐标.
在 中, , , 是 边上一点,且 , 是 的中点, 是 的中线.
(1)如图 ,连接 ,请直接写出 和 的数量关系: ;
(2)点 是射线 上的一个动点,将射线 绕点 逆时针旋转得射线 ,使 , 与射线 交于点 .
①如图 ,猜想并证明线段 和线段 之间的数量关系;
②若 , ,当 时,请直接写出线段 的长度(用含 的代数式表示).

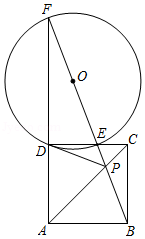
如图,点 为正方形 的对角线 上的一点,连接 并延长交 于点 ,交 的延长线于点 , 是 的外接圆,连接 .
(1)求证: 是 的切线;
(2)若 ,正方形 的边长为4,求 的半径和线段 的长.
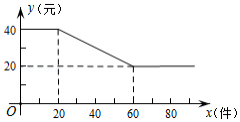
某工厂生产一种火爆的网红电子产品,每件产品成本16元、工厂将该产品进行网络批发,批发单价 (元 与一次性批发量 (件 为正整数)之间满足如图所示的函数关系.
(1)直接写出 与 之间所满足的函数关系式,并写出自变量 的取值范围;
(2)若一次性批发量不超过60件,当批发量为多少件时,工厂获利最大?最大利润是多少?