如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F。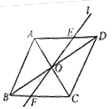
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度。
(1)解方程:
(2)x,y表示两个数,规定新运算“*”及“”如下:x*y=mx+ny,x△y=kxy,其中m,n,k均为自然数(零除外),已知1*2=5,(2*3)△4=64,求(1△2)*3的值.
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①请直接写出图1中线段BG、线段DE的数量关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度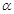 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.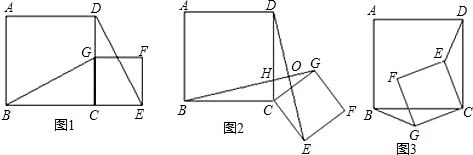
(2)将原题中正方形改为矩形(如图4~6),且 ,试判断(1)①中得到的结论哪个成立,哪个不成立?(写出你的判断,不必证明.)
,试判断(1)①中得到的结论哪个成立,哪个不成立?(写出你的判断,不必证明.)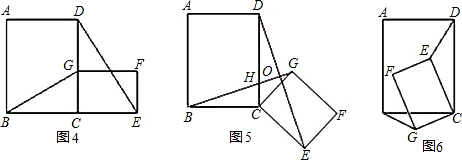
(3)在图5中,连结DG、BE,且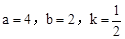 ,则
,则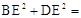 .
.
阅读材料:已知方程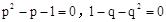 且
且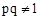 ,求
,求 的值.
的值.
解:由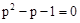 ,及
,及 可知
可知 ,又∵
,又∵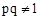 ,∴
,∴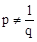 .
.
∵ 可变形为
可变形为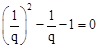 ,根据
,根据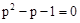 和
和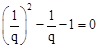 的特征.
的特征.
∴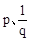 是方程
是方程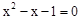 的两个不相等的实数根,则
的两个不相等的实数根,则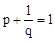 ,即
,即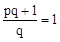 .
.
根据阅读材料所提供的方法,完成下面的解答.
已知: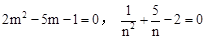 ,且
,且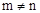 ,求下列各式的值(1)
,求下列各式的值(1)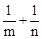 ;(2)
;(2)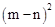 .
.
定义:如图,若双曲线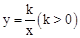 与它的其中一条对称轴
与它的其中一条对称轴 相交于两点A,B,则线段AB的长称为双曲线
相交于两点A,B,则线段AB的长称为双曲线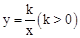 的对径.
的对径.
(1)求双曲线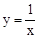 的对径;
的对径;
(2)若某双曲线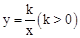 对径是
对径是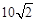 .求k的值;
.求k的值;
(3)仿照上述定义,请你定义双曲线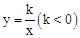 的对径.
的对径.
已知关于x的方程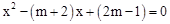 .
.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是3,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.