已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.
某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球作圆周运动,由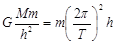 得
得
⑴请判断上面的结果是否正确,并说明理由.如不正确,请给出正确的解法和结果.
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
已知金属铯的逸出功为1.9 eV,在光电效应实验中,要使铯表面发出的光电子的最大初动能为1.0 eV,求入射光的波长应为多少?
两磁铁各放在一辆小车上,小车能在水平面上无摩擦地沿同一直线运动.已知甲车和磁铁的总质量为0.5 kg,乙车和磁铁的总质量为1 kg.两磁铁的N极相对,推动一下,使两车相向运动.某时刻甲的速率为2 m/s,乙的速率为3 m/s,方向与甲相反.两车运动过程中始终未相碰.求:
(1)两车最近时,乙的速度为多大?
(2)甲车开始反向运动时,乙的速度为多大?
一置于桌面上质量为M的玩具炮,水平发射质量为m的炮弹.炮可在水平方向自由移动.当炮身上未放置其他重物时,炮弹可击中水平地面上的目标A;当炮身上固定一质量为M0的重物时,在原发射位置沿同一方向发射的炮弹可击中水平地面上的目标B.炮口离水平地面的高度为h.如果两次发射时“火药”提供的机械能相等,求B、A两目标与炮弹发射点之间的水平距离之比.
火箭喷气发动机每次喷出m=0.2 kg的气体,喷出的气体相对地面的速度v=1000 m/s.设火箭的初质量M=300 kg,发动机每秒喷气20次,在不考虑地球引力及空气阻力的情况下,火箭在1 s末的速度是多大?
如图14-1-8所示,高h=0.45 m的光滑水平桌面上有质量m1=2 kg的物体,以水平速度v1=5 m/s向右运动,与静止的另一质量m2=1 kg的物体相碰.若碰撞后m1仍向右运动,速度变为v1′=3 m/s,求:(不计空气阻力,g=10 m/s2)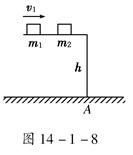
(1)m2落地时距桌边缘A点的水平距离;
(2)m2落地时动量的大小.