已知P是双曲线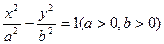
的右支上一点，A1，A2分别为双曲线的左、右顶点，F1，F2分别为双曲线的左、右焦点，双曲线的离心率为e，有下列命题
①双曲线的一条准线被它的两条渐近线所截得的线段长度为
②若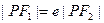
，则e的最大值为
③
的内切圆的圆心横坐标为a；
④若直线PF1的斜率为k，则
其中正确的命题的序号是
若函数y=x3+ax2+bx+27在x=－1时有极大值，在x=3时有极小值，则a=______b=______
设x、y满足约束条件
则
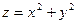的最小值是
某区高二年级的一次数学统考中，随机抽取
200名同学的成绩，成绩全部在50分至100
分之间，将成绩按下方式分成5组；第一组，
成绩大于等于50分且小于60分；第二组，
成绩大于等于60分且小于70分；……第五
组，成绩大于等于90分且小于等于100分。
据此绘制了如图所示的频率分布直方图。
则这200名同学中成绩大于等于80分且小于
90分的学生有名
（请考生在以下三个小题中任选一题
做答，如果多做，则按所做的第一题评阅记分）
（1）（选修4—4坐标系与参数方程）
已知曲线C的极坐标方程是
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线
的参数方程是
，则直线与曲线C相交所成弦的弦长为
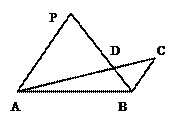（2）（选修4—5 不等式选讲）已知
，且
，则
的最小值为
（3）(选修4—1 几何证明选讲）如图,若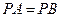
，
，
与
交于点D
且
，
，则