将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面长为hcm,则h的取值范围是什么?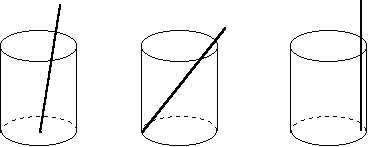
将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm。
(1)求10张白纸粘合后的长度;
(2)设x张白纸粘合后的总长为ycm,写出y与x的函数关系式。
八年级一、二班举行投篮比赛,每班各挑选10名同学代表班级参加7轮积分赛,投篮命中率如下:
| 场次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 一班 |
85% |
88% |
77% |
75% |
85% |
80% |
70% |
| 二班 |
90% |
85% |
70% |
80% |
60% |
83% |
92% |
你认为哪个班级的投篮命中率较稳定?为什么?