已知：关于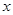
的一元一次方程
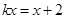①的根为正实数，一元二次方程
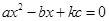有一实数根
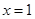
若方程①的根为正整数，求整数
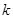的值求代数式
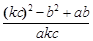的值求证：关于
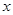的一元二次方程 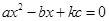②必有两个不相等的实数根。
观察下列等式：
，
，
，
将以上三个等式两边分别相加得：
．
（1）猜想并写出：
= ．
（2）直接写出下列各式的计算结果：
①
= ；
②
；
（3）探究并计算：
．
如果方程5（x-3）=4x-10的解与方程4x-（3a+1）=6x+2a-1的解相同，求式子（2a2+3a-4）-（-3a2+7a-1）的值．
已知有理数a，b在数轴上的位置如图：
（1）在数轴上标出-a，-b的位置，并将a，b，-a，-b用“＜”连接；
（2）化简|a+b|-|a-b|-|a|．
已知：A-2B=7a2-7ab，且B=-3a2+6ab+4．
（1）求A等于多少？
（2）若|a+b-1|+（b-2）2=0，求A的值．
解方程：
（1）4x-3（20-x）+4=0
（2）
．