若一次函数 (
( 是常数)与
是常数)与 (
( 是常数),满足
是常数),满足 且
且 ,则称这两函数是对称函数
,则称这两函数是对称函数当函数
 与
与 是对称函数,求
是对称函数,求 和
和 的值;
的值;在平面直角坐标系中,一次函数
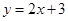 图象与
图象与 轴交于点
轴交于点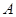 、与
、与 轴交于点
轴交于点 ,点
,点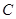 与点
与点 关于x轴对称,过点
关于x轴对称,过点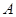 、
、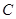 的直线解析式是
的直线解析式是 ,求证:函数
,求证:函数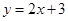 与
与 是对称函数
是对称函数
如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求出在这两次变换过程中,点A经过点A1到达A2的路径总长.

先化简,再求值: ,其中 .
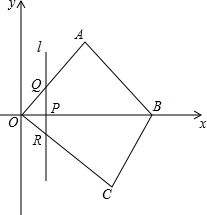
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上. 且 ,OB,OC的长分别是一元二次方程 的两个根 .
(1)求点A和点B的坐标.
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知 时,直线l恰好过点C.当 时,求m关于t的函数关系式.
(3)当 时,请直接写出点P的坐标.
“全民阅读”深入人心,读好书让人终身受益.为打造书香校园,满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和科技阅读两类图书.经了解,20本文学名著和40本科技阅读共需1520元,一本文学名著比一本科技阅读多22元(注:所采购的文学名著书价格都一样,所采购的科技阅读书价格都一样).
(1)求每本文学名著和科技阅读各多少元?
(2)若学校要求购买科技阅读比文学名著多20本,科技阅读和文学名著总数不低于72本,总费用不超过2000元,请你为学校求出符合条件的购书方案.
(3)请在(2)的条件下,请你求出此次活动学校最多需投入资金多少元?
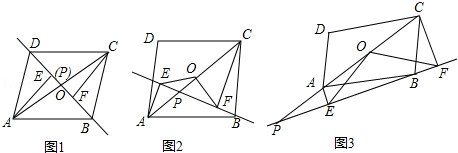
已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.