(本题满分14分)抽样调查30个工人的家庭人均月收入,得到如下数据:(单位:元)
404 444 556 430 380 420 500 430 420 384 420 404 424 340 424 412 388 472 358 476 376 396 428 444 366 436 364 438 330 426
(1)取组距为60,起点为320,列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计人均月收入在[440,500)中的家庭所占的百分比.
(本小题满分14分)
已知函数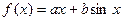 ,当
,当 时,
时, 取得极
取得极 小值
小值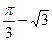 .
.
(1)求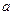 ,
,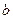 的值;
的值;
(2)设直线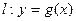 ,曲线
,曲线 .若直线
.若直线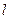
 与曲线
与曲线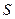 同时满足下列两个条件:
同时满足下列两个条件:
①直线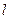 与曲线
与曲线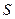 相切且至少有两个
相切且至少有两个 切点;
切点;
②对任意 都有
都有 .则称直线
.则称直线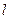 为曲线
为曲线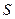 的“上夹线”.
的“上夹线”.
试证明:直线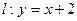 是曲线
是曲线 的“上夹线”.
的“上夹线”.
(3)记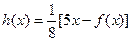 ,设
,设 是方程
是方程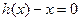 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的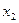 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数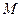 ,使得
,使得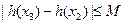 恒成立,若存在请求出
恒成立,若存在请求出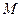 的值;若不存在请说明理由.
的值;若不存在请说明理由.
(本小题满分13分)
已知抛物线 :
: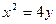 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线
交抛物线 于
于 、
、 两点;椭圆
两点;椭圆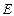 的中心在原点,焦点在
的中心在原点,焦点在 轴上,点
轴上,点 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率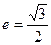 .
.
(1)求椭圆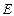 的方程;
的方程;
(2)经过 、
、 两点分别作抛物线
两点分别作抛物线 的切线
的切线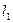 、
、 ,切线
,切线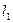 与
与 相交于点
相交于点 .证明:
.证明: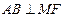 ;
;
(3) 椭圆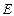 上是否存在一点
上是否存在一点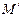 ,经过点
,经过点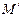 作抛物线
作抛物线 的两条切线
的两条切线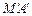 、
、 (
(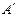 、
、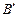 为切点),使得直线
为切点),使得直线 过点
过点 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线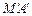 、
、 所围成图形的面积;若不存在,试说明理由
所围成图形的面积;若不存在,试说明理由 .
.
执行下面框图所描述的算法程序,记输出的一列数依次为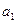 ,
,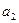 ,…,
,…,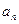 ,
,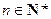 ,
,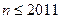 .
.
(1)若输 入
入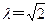 ,写出输出结果;
,写出输出结果;
(2)若输入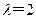 ,求数列
,求数列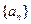 的通项公式;
的通项公式;
(3)若输入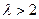 ,令
,令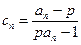 ,求常数
,求常数 (
(
 ),使得
),使得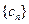 是等比数列.
是等比数列.
(本小题满分12分)
一个几何体是由圆柱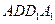 和
和 三棱锥
三棱锥 组合而成,点
组合而成,点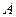 、
、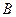 、
、 在圆
在圆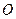 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中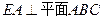 ,
,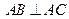 ,
,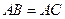 ,
,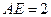 .
.
(1)求证: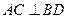 ;
;
(2)求二面角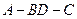 的平面角的大小.
的平面角的大小.
(本小题满分12分)
为了评估天气对大运会的影响,制定相应预案,深圳市气象局通过对最近50多年的气象数据资料的统计分析,发现8月份是本市雷电天气高峰期,在31天中平均发生雷电14.57天如图 .如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
.如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.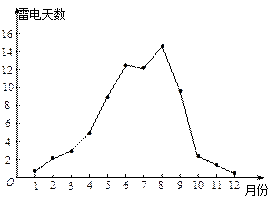
(1)求在大运会开幕(8月12日)后的前3天比赛中,恰好有2天发生雷电天气的概率(精确到0.01);
(2)设大运会期间(8月12日至23日,共12天),发生雷电天气的天数为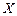 ,求
,求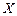 的数学期望和方差.
的数学期望和方差.