(本小题满分15分)为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民用户电价为每千瓦时为0.53元.若总用电量为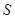 千瓦时,设高峰时段用电量为
千瓦时,设高峰时段用电量为 千瓦时.
千瓦时.
(1)写出实行峰谷电价的电费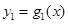 及现行电价的电费的
及现行电价的电费的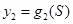 函数解析式及电费总差额
函数解析式及电费总差额 的解析式;
的解析式;
(2)对于用电量按时均等的电器(在全天任何相同长的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?说明你的理由.
本小题满分14分)
已知 的顶点坐标为
的顶点坐标为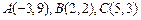
(1)求 边的长
边的长
(2)求 边中线所在直线的方程
边中线所在直线的方程
(3)求 的面积
的面积
(本小题满分12分)
已知函数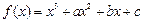 在
在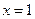 处的切
处的切 线方程为
线方程为 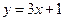 ,
,
(1)若函数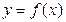 在
在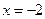 时有极值,求
时有极值,求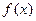 的表达式;
的表达式;
(2)在(1)条件下,若函数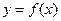 在
在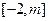 上的值域为
上的值域为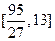 ,求m的取值范围;
,求m的取值范围;
(3)若函数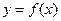 在区间
在区间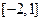 上
上 单调递增,求b的取值范围.
单调递增,求b的取值范围.
(本小题满分12分)
已知数列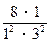 ,
,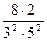 ,…,
,…,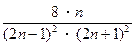 ,…。S
,…。S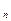 为其前n项和,
为其前n项和,
求S 、S
、S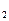 、S
、S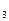 、S
、S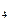 ,推测S
,推测S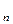 公式,并用数学归纳法证明。
公式,并用数学归纳法证明。
(本小题满分12分)
某工厂生产一种精密仪器, 产品是否合格需先后经过两道相互独立的工序检查,且当第一道工序检查合格后才能进入到第二道工序,经长期检测发现,该仪器第一道工序检查合格的概率为 ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 ,已知该厂每月生产3台这种仪器.
,已知该厂每月生产3台这种仪器.
(1)求生产一台合格仪器的概率;
(2)用 表示每月生产合格仪器的台数,求
表示每月生产合格仪器的台数,求 的分布列和数学期望;
的分布列和数学期望;
(3)若生产一台合格仪器可盈利10万元,不合格要亏损3万元,求该厂每月的期望盈利额.
(本小题满分10分)
已知二项式 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;
的值;
(2)设 .
.
①求 的值;
的值;
②求 的值;
的值;
③求 的最大值.
的最大值.