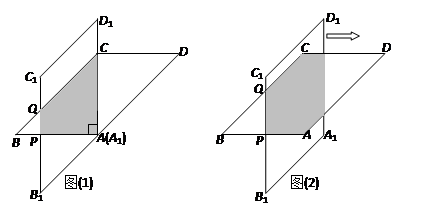
已知：如图(1)，在平行四边形ABCD中，对角线CA⊥BA，AB＝AC＝8cm，四边形A1B1C1D1是平行四边形ABCD绕点A按逆时针方向旋转45°得到的，A1D1经过点C，B1C1分别与AB、BC相交于点P、Q．
（1）求四边形CD1C1Q的周长；(保留无理数，下同)
（2）求两个平行四边形重合部分的四边形APQC的面积S；
（3）如图(2)，将平行四边形A1B1C1D1以每秒1cm的速度向右匀速运动，当运动到B1C1在直线AC上时停止运动．设运动的时间为x（秒），两个平行四边形重合部分的面积为y（cm2）．求y关于x的函数关系式，并探索是否存在一个时刻x，使得y取最大值，若存在，请你求出这个最大值；若不存在，请你说明理由．
直线y＝
x＋2与x轴、y轴分别交于A、B两点，D是x轴上一点，坐标为（x，0），△ABD的面积为S.
（1）求点A和点B的坐标；
（2）求S与x的函数关系式；
（3）当S=12时，求点D的坐标.
下面的表格是李刚同学一学期数学成绩的记录，根据表格提供的信息回答下面的问题
（1）李刚同学6次成绩的极差是 ．
（2）李刚同学6次成绩的中位数是 ．
（3）李刚同学平时成绩的平均数是 ．
（4）利用图的权重计算一下李刚本学期的综合成绩（平时成绩用四次成绩的平均数写出解题过程，每次考试满分都是100分）
已知圆O的直径AB、CD互相垂直，弦AE交CD于F，若圆O的半径为R.
求证：AE·AF＝2 R
.
如图，有一长方形的地，长为x米，宽为120米，建筑商将它分成三部分：甲、乙、丙.甲和乙为正方形.现计划甲建设住宅区，乙建设商场，丙开辟成公司.若已知丙地的面积为3200平方米，试求x的值.
人在运动时的心跳速率通常和人的年龄有关.如果用a表示一个人的年龄，用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么b=0.8(220-a).
（1）正常情况下,在运动时一个14岁的少年所能承受的每分钟心跳的最高次数是多少？
（2）一个45岁的人运动时10秒心跳的次数为22次，请问他有危险吗？为什么？