乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换。每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立。甲、乙的一局比赛中,甲先发球。
(Ⅰ)求开始第4次发球时,甲、乙的比分为1比2的概率;
(Ⅱ)
表示开始第4次发球时乙的得分,求
的期望。
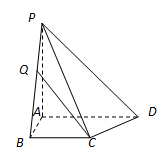
【2015江苏高考,22】(本小题满分10分)如图,在四棱锥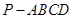 中,已知
中,已知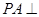 平面
平面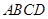 ,且四边形
,且四边形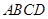 为直角梯形,
为直角梯形,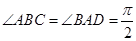 ,
,
(1)求平面 与平面
与平面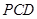 所成二面角的余弦值;
所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成角最小时,求线段BQ的长
【2015高考安徽,理19】如图所示,在多面体 ,四边形
,四边形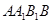 ,
, 均为正方形,
均为正方形, 为
为 的中点,过
的中点,过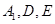 的平面交
的平面交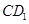 于F.
于F.
(Ⅰ)证明: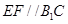 ;
;
(Ⅱ)求二面角 余弦值.
余弦值.
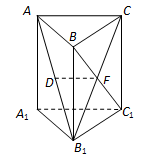
【2015江苏高考,16】如图,在直三棱柱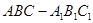 中,已知
中,已知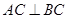 ,
,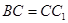 ,设
,设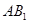 的中点为
的中点为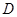 ,
,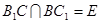 .
.
求证:(1)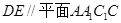 ;
;
(2)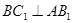 .
.
【2015高考新课标2,理19】
如图,长方体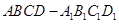 中,
中,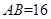 ,
, ,
,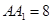 ,点
,点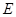 ,
,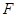 分别在
分别在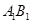 ,
,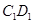 上,
上,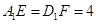 .过点
.过点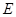 ,
,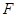 的平面
的平面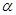 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.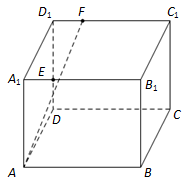
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线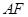 与平面
与平面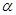 所成角的正弦值.
所成角的正弦值.
【2015高考上海,理21】已知椭圆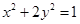 ,过原点的两条直线
,过原点的两条直线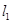 和
和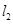 分别于椭圆交于
分别于椭圆交于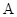 、
、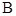 和
和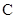 、
、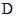 ,记得到的平行四边形
,记得到的平行四边形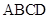 的面积为
的面积为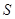 .
.
(1)设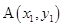 ,
,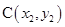 ,用
,用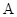 、
、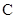 的坐标表示点
的坐标表示点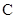 到直线
到直线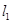 的距离,并证明
的距离,并证明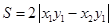 ;
;
(2)设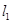 与
与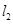 的斜率之积为
的斜率之积为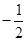 ,求面积
,求面积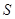 的值.
的值.