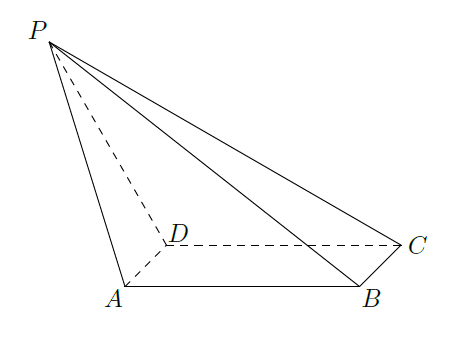
如图,在四棱锥
中,底面
是矩形,
,
,
,
.
(1)求异面直线
与
所成角的正切值;
(2)证明平面
平面
(3)求直线
与平面
所成角的正弦值。
若两集合 ,
, , 分别从集合
, 分别从集合 中各任取一个元素
中各任取一个元素 、
、 ,即满足
,即满足 ,
, ,记为
,记为 ,
,
(Ⅰ)若 ,
, ,写出所有的
,写出所有的 的取值情况,并求事件“方程
的取值情况,并求事件“方程 所对应的曲线表示焦点在
所对应的曲线表示焦点在 轴上的椭圆”的概率;
轴上的椭圆”的概率;
(Ⅱ)求事件“方程 所对应的曲线表示焦点在
所对应的曲线表示焦点在 轴上的椭圆,且长轴长大于短轴长的
轴上的椭圆,且长轴长大于短轴长的 倍”的概率.
倍”的概率.
已知定义在R上的函数f(x)= -2x3+bx2+cx(b,c∈R),函数F(x)=f(x)-3x2是奇函数,函数f(x)在x= -1处取极值.
(Ⅰ)求f(x)的解析式;
(Ⅱ)讨论f(x)在区间[-3,3]上的单调性.
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表: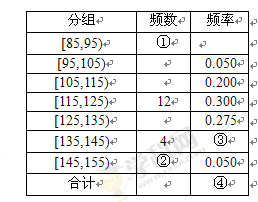
(Ⅰ)①②③④处的数值分别为________、________、________、________;
(Ⅱ)在所给的坐标系中画出区间[85,155]内的频率分布直方图;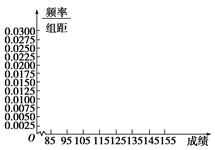
(Ⅲ) 现在从成绩为[135,145)和[145,155) 的两组学生中选两人,求他们同在[135,145)分数段的概率。
直线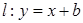 与抛物线
与抛物线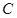
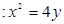 相切于点A.
相切于点A.
(Ⅰ) 求实数 的值,及点A的坐标;
的值,及点A的坐标;
(Ⅱ) 求过点B(0,-1)的抛物线 的切线方程。
的切线方程。
一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数 时,输出结果记为
时,输出结果记为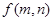 ,且计算装置运算原理如下:①若Ⅰ、Ⅱ分别输入1,则
,且计算装置运算原理如下:①若Ⅰ、Ⅱ分别输入1,则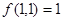 ;②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍。
;②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:(1)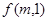 的表达式
的表达式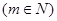 ;
;
(2)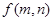 的表达式
的表达式 ;
;
(3)若Ⅰ、Ⅱ都输入正整数 ,则输出结果
,则输出结果 能否为2013?
能否为2013?
若能,求出相应的 ;若不能,则请说明理由。
;若不能,则请说明理由。