铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次，记录如下：
| 学生 |
8次测试成绩 |
平均数 |
中位数 |
方差 |
|||||||
| 甲 |
95 |
82 |
88 |
81 |
93 |
79 |
84 |
78 |
85 |
|
35.5 |
| 乙 |
83 |
92 |
80 |
95 |
90 |
80 |
85 |
75 |
|
84 |
|
（1） 请你在表中填上甲、乙两名学生这8次测试成绩的平均数、中位数和方差。（其中平均数和方差的计算要有过程）
（2） 现要从中选派一人参加操作技能大赛，从统计学的角度考虑，你认为选派哪名同学参加合适，请说明理由。
如图，在直角坐标系中，A(0，4)、C(3，0)，
（1）① 画出线段AC关于y轴对称线段AB；
② 将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD；
（2）若直线y＝kx平分(1)中四边形ABCD的面积，请直接写出实数k的值.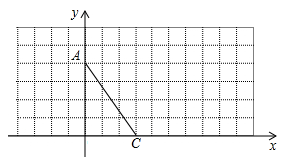
如图，
和
相交于点
，
，
，求证：
.
已知直线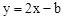
经过点(1，－1)，求关于x的不等式2x－b≥0的解集.
解方程：
.
如图，已知抛物线
与x轴的交点为A、D（A在D的右侧），与y轴的交点为C.
（1）直接写出A、D、C三点的坐标；
（2）在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；
（3）设点C关于抛物线对称的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由.