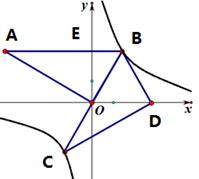
若一次函数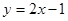
和反比例函数
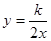的图象都经过点（1，1）（1）求反比例函数的解析式.（2）已知点
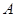在第三象限，且同时在两个函数的图像上，求点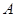的坐标.（3）利用（2）的结果，若点
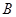的坐标为（2，0），且以点,
,,
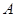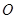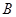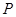为顶点的四边形是平行四边形，请你直接写出点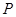的坐标.
如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴和y轴的正半轴上，顶点B的坐标为（2m，m），翻折矩形OABC，使点A与点C重合，得到折痕DE．设点B的对应点为F，折痕DE所在直线与y轴相交于点G，经过点C、F、D的抛物线为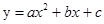
．
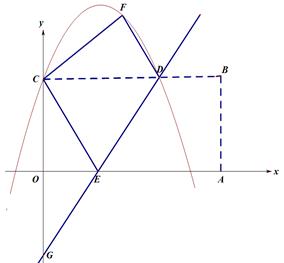
（1）求点D的坐标（用含m的式子表示）
（2）若点G的坐标为（0，-3），求该抛物线的解析式．
（3）在（2）的条件下，设线段CD的中点为M，在线段CD上方的抛物线上是否存在点P，使PM=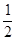
EA?若存在，直接写出P的坐标，若不存在，说明理由．
如图，在
中，点
、
、
分别在
、
、
上，且
，
．
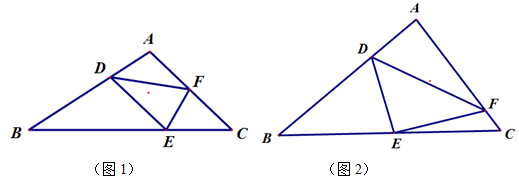
（1）如图1，当
时，图1中是否存在于
相等的线段？若存在，请找出并加以证明．若不存在说明理由．
（2）如图2，当
（其中
）时，若
，
，求
的长（用含
，
的式子表示）．
如图1，在△ABC中，∠C=90°，点D在AC上，且CD>DA，DA=2．点P、Q同时从D点出发，以相同的速度分别沿射线DC、射线DA运动．过点Q作AC的垂线段QR，使QR=PQ，联接PR．当点Q到达A时，点P、Q同时停止运动．设PQ=x．△PQR和△ABC重合部分的面积为S．S关于x的函数图像如图2所示（其中0<x≤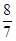
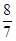，<x≤m时，函数的解析式不同）
（1）填空：n的值为___________;
（2）求S关于x的函数关系式，并写出x的取值范围．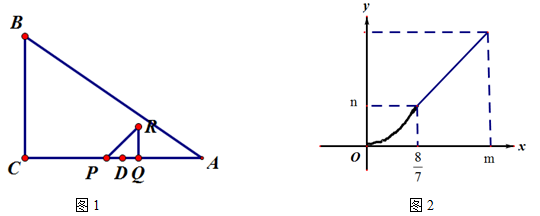
如图，AB是圆O的直径，点C、D在圆O上，且AD平分∠CAB．过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F．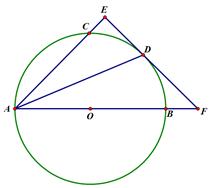
（1）求证：EF与圆O相切；
（2）若AB=6，AD=4
，求EF的长．
如图，在平面坐标系中，∠AOB=90°，AB∥x轴，OB=2，双曲线y=
经过点B．将△AOB绕点B逆时针旋转，使点O的对应点D落在X轴的正半轴上．若AB的对应线段CB恰好经过点O．
点B的坐标和双曲线的解析式．
判断点C是否在双曲线上，并说明理由．