先化简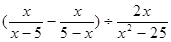 ,然后从不等组
,然后从不等组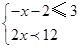 的解集中,选取一个你认为符合题意的x的值代入求值.
的解集中,选取一个你认为符合题意的x的值代入求值.
为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图),请你用尺规作图的方法确定点P的位置.(要求: 写出已知、求作;不写作法,保留作图痕迹,必须用铅笔作图)
如图,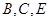 三点在同一条直线上,
三点在同一条直线上, ∥
∥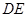 ,
, 。求证:△ABC≌△CDE。
。求证:△ABC≌△CDE。
解方程: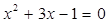
如图,已知直线 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
(1)填空:点A的坐标为,点B的坐标为,AB的长为.
(2)求点C、D的坐标
(3)求抛物线的解析式
(4)若抛物线与正方形沿射线AB下滑,直至点C落在
 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为.
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为.