一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
如图,在△ABC中,D、E两点分别在AB和AC上,求证CD、BE不可能互相平分.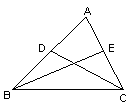
已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上.
已知:如图等边 内接于⊙O,点
内接于⊙O,点 是劣弧
是劣弧 上的一点(端点除外),延长
上的一点(端点除外),延长 至
至 ,使
,使 ,连结
,连结 .
.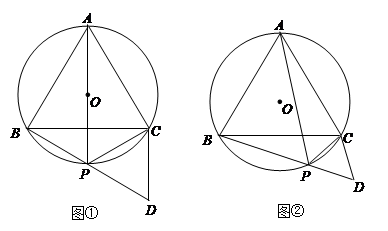
(1)若 过圆心
过圆心 ,如图①,请你判断
,如图①,请你判断 是什么三角形?并说明理由.
是什么三角形?并说明理由.
(2)若 不过圆心
不过圆心 ,如图②,
,如图②,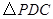 又是什么三角形?为什么?
又是什么三角形?为什么?
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的半径。
如图所示,已知AB为⊙O的直径,CD是弦,且AB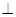 CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.
(1)求证: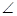 ACO=
ACO=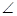 BCD.
BCD.
(2)若EB= ,CD=
,CD=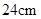 ,求⊙O的直径.
,求⊙O的直径.