先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
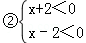
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
(1)一元二次不等式x2﹣16>0的解集为 ;
(2)分式不等式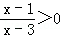 的解集为 ;
的解集为 ;
(3)解一元二次不等式2x2﹣3x<0.
如图(a)过反比例函数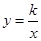 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S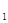 与S
与S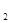 ,
,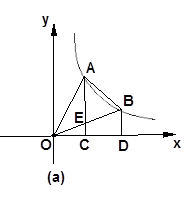
试比较S
 与S
与S 的大小;
的大小;如图(b),已知直线
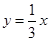 与双曲线
与双曲线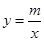 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.
①求m的值;
②若过原点的另一条直线l交双曲线于P、Q两点(P点在第一象限),若由M、N、P、Q为顶点组成的四边形面积为64,求P点的坐标。
已知二次函数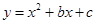 的图象过点A(-3,0)和点B(1,0),且与
的图象过点A(-3,0)和点B(1,0),且与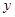 轴交于点C,D点在抛物线上且横坐标是 -2。
轴交于点C,D点在抛物线上且横坐标是 -2。
求抛物线的解析式;
抛物线的对称轴上有一动点P,求出PA+PD的最小值
点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E、G点坐标;如果不存在,请说明理由。
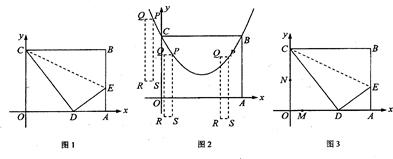
如图1,矩形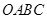 的顶点
的顶点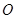 为原点,点
为原点,点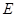 在
在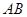 上,把
上,把 沿
沿 折叠,使点
折叠,使点 落在
落在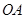 边上的点
边上的点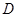 处,点
处,点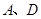 坐标分别为
坐标分别为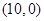 和
和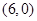 ,抛物线
,抛物线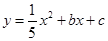 过点
过点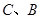 .
.
求
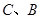 两点的坐标及该抛物线的解析式;
两点的坐标及该抛物线的解析式;如图2,长、宽一定的矩形
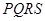 的宽
的宽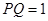 ,点
,点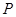 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中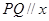 轴,且
轴,且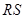 在
在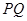 的下方,当
的下方,当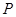 点横坐标为-1时,点
点横坐标为-1时,点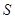 距离
距离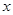 轴
轴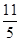 个单位,当矩形
个单位,当矩形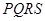 在滑动过程中被
在滑动过程中被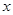 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点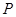 的坐标;
的坐标;如图3,动点
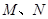 同时从点
同时从点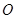 出发,点
出发,点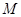 以每秒3个单位长度的速度沿折线
以每秒3个单位长度的速度沿折线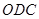 按
按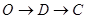 的路线运动,点
的路线运动,点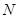 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线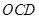 按
按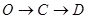 的路线运动,当
的路线运动,当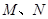 两点相遇时,它们都停止运动.设
两点相遇时,它们都停止运动.设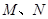 同时从点
同时从点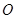 出发
出发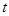 秒时,
秒时,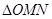 的面积为
的面积为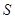 .①求出
.①求出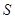 与
与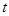 的函数关系式,并写出
的函数关系式,并写出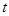 的取值范围:②设
的取值范围:②设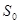 是①中函数
是①中函数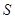 的最大值,那么
的最大值,那么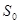 =.
=.
如图,直线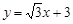 分别交
分别交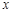 轴、
轴、 轴于B、A两点,抛物线L:
轴于B、A两点,抛物线L: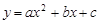 的顶点G在
的顶点G在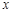 轴上,且过(0,4)和(4,4)两点.
轴上,且过(0,4)和(4,4)两点.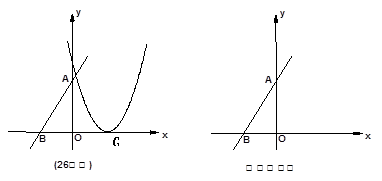
求抛物线L的解析式;
抛物线L上是否存在这样的点C,使得四边形ABGC是以BG为底边的梯形,若存在,请求出C点的坐标,若不存在,请说明理由.
将抛物线L沿
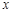 轴平行移动得抛物线L
轴平行移动得抛物线L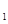 ,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L
,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L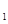 上. 试问这样的抛物线L
上. 试问这样的抛物线L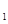 是否存在,若存在,求出L
是否存在,若存在,求出L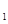 对应的函数关系式,若不存在,说明理由.
对应的函数关系式,若不存在,说明理由.
已知,抛物线 与x轴交于
与x轴交于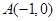 和
和 两点,与y轴交于
两点,与y轴交于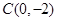 。
。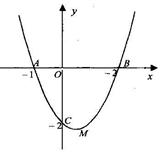
求这条抛物线的解析式和抛物线顶点M的坐标
求四边形ABMC的面积;
在对称轴的右侧的抛物线上是否存在点P,使
 为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由
为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由