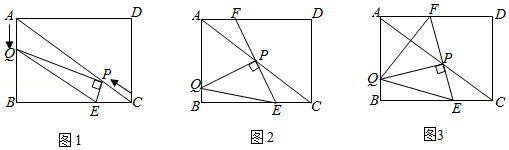
如图1,在矩形 中, , ,动点 , 分别从 点, 点同时以每秒1个单位长度的速度出发,且分别在边 , 上沿 , 的方向运动,当点 运动到点 时, , 两点同时停止运动.设点 运动的时间为 ,连接 ,过点 作 , 与边 相交于点 ,连接 .
(1)如图2,当 时,延长 交边 于点 .求证: ;
(2)在(1)的条件下,试探究线段 , , 三者之间的等量关系,并加以证明;
(3)如图3,当 时,延长 交边 于点 ,连接 ,若 平分 ,求 的值.
如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,
A点在C处的北偏西45°方向,求∠BAC及∠BCA的度数?
在平面直角坐标系中,顺次连结A(-2,0)、B(4,0)、C(-2,-3)各点,试求:
(1)A、B两点之间的距离。
(2)点C到X轴的距离。
(3)△ABC的面积。
如图15,抛物线 与
与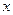 轴交于
轴交于 两点,与
两点,与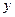 轴交于点
轴交于点 ,连结
,连结 ,若
,若
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴 上是否存在点
上是否存在点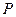 ,使
,使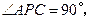 若存在,求出点
若存在,求出点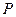 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图16所示,连结 ,
, 是线段
是线段 上(不与
上(不与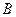 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的横坐标为
的横坐标为 .当t为何值时,
.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
已知:如图14,⊙A与 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.
已知两个全等的直角三角形纸片 、
、 ,如图11放置,点
,如图11放置,点 、
、 重合,点
重合,点 在
在 上,
上, 与
与 交于点
交于点 .
. ,
, ,
, .
.
(1)求证: 是等腰三角形;
是等腰三角形;
(2)若纸片 不动,若
不动,若 绕点
绕点 逆时针旋转.问首次使四边形
逆时针旋转.问首次使四边形 成为以
成为以 为底的梯形时,(如图12).旋转角α的度数是度,并请你求出此时梯形的高.
为底的梯形时,(如图12).旋转角α的度数是度,并请你求出此时梯形的高.