(8分)一个口袋有5个同样大小的球,编号为1、2、3、4、5,从中同时取出3个,以ξ表示取出球编号的最小号码,求(1)ξ的分布列.(2)取出球编号最小的号码小于等于2的概率
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
处罚金额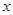 (元) (元) |
0 |
5 |
10 |
15 |
20 |
会闯红灯的人数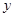 |
80 |
50 |
40 |
20 |
10 |
若用表中数据所得频率代替概率.现从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
(Ⅰ)求这两种金额之和不低于20元的概率;
(Ⅱ)若用X表示这两种金额之和,求X的分布列和数学期望.
数列 的前
的前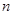 项和记为
项和记为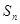 ,已知
,已知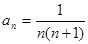 .
.
(Ⅰ)求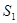 ,
,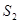 ,
,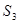 的值,猜想
的值,猜想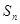 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明你的猜想.
已知极坐标的极点在平面直角坐标系的原点O处,极轴与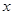 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线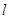 的极坐标方程为:
的极坐标方程为: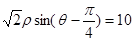 ,曲线C:
,曲线C: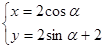 (
(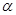 为参数),其中
为参数),其中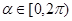 .
.
(Ⅰ)试写出直线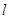 的直角坐标方程及曲线C的普通方程;
的直角坐标方程及曲线C的普通方程;
(Ⅱ)若点P为曲线C上的动点,求点P到直线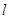 距离的最大值.
距离的最大值.
已知复数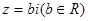 ,
,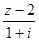 是实数,
是实数,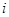 是虚数单位.
是虚数单位.
(1)求复数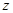 ;
;
(2)若复数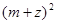 所表示的点在第一象限,求实数
所表示的点在第一象限,求实数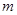 的取值范围.
的取值范围.
已知关于x的不等式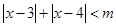 的解集不是空集.
的解集不是空集.
(1)求参数m的取值范围的集合M;
(2)设a,b M,求证:a+b<ab+1.
M,求证:a+b<ab+1.