古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两个工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲: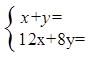 乙:
乙: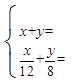
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示____________________,y表示 __________________;
乙:x表示 ____________________,y表示 __________________;
(2)求A、B两工程队分别整治河道多少米?(写出完整的解答过程)
已知:如图,AB是⊙O的直径,点C.D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
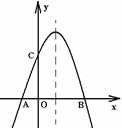
如图,抛物线的对称轴是直线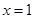 ,它与
,它与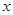 轴交于
轴交于 ,
,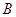 两点,与
两点,与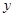 轴交于
轴交于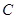 点,点
点,点 ,
,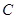 的坐标分别是
的坐标分别是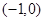 ,
,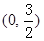 .
.
(1) 求此抛物线对应的函数解析式;
(2) 若点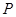 是抛物线上位于
是抛物线上位于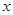 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.
如图,△ABC内接于半圆,AB为直径,设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
求证:FD=FG.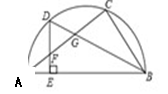
如图1,抛物线y= -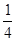 x2+
x2+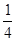 x+3与x轴交于A.C两点,与y轴交于B点,与直线y=kx+b交于A.D两点.
x+3与x轴交于A.C两点,与y轴交于B点,与直线y=kx+b交于A.D两点.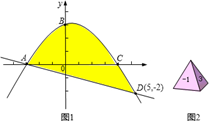
(1)直接写出A、C两点坐标和直线AD的解析式;
(2)如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1.1.3.4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点P(m,n)落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
已知抛物线的顶点(-1,-2)且图象经过(1,6),求此抛物线解析式.
(1)求该二次函数的解析式;
(2)当y>0时,x的取值范围.