已知:如图,AB是⊙O的直径,点C.D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品 (吨),生产甲、乙两种产品获得的总利润为 (万元).
(1)求 与 之间的函数表达式;
(2)若每生产1吨甲产品需要 原料0.25吨,每生产1吨乙产品需要 原料0.5吨.受市场影响,该厂能获得的 原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
如图,在 中, .将 沿着 方向平移得到 ,其中点 在边 上, 与 相交于点 .
(1)求证: 为等腰三角形;
(2)连接 、 、 ,当点 在什么位置时,四边形 为矩形,并说明理由.

现有 、 、 三个不透明的盒子, 盒中装有红球、黄球、蓝球各1个, 盒中装有红球、黄球各1个, 盒中装有红球、蓝球各1个,这些球除颜色外都相同.现分别从 、 、 三个盒子中任意摸出一个球.
(1)从 盒中摸出红球的概率为 ;
(2)用画树状图或列表的方法,求摸出的三个球中至少有一个红球的概率.
为了解某地区中学生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内, 小时(含2小时), 小时(含4小时),6小时及以上,并绘制了如图所示尚不完整的统计图.
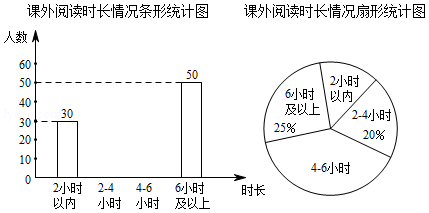
(1)本次调查共随机抽取了 名中学生,其中课外阅读时长“ 小时”的有 人;
(2)扇形统计图中,课外阅读时长“ 小时”对应的圆心角度数为 ;
(3)若该地区共有20000名中学生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
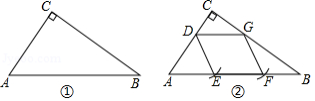
如图①,在 中, , , .求作菱形 ,使点 在边 上,点 、 在边 上,点 在边 上.
小明的作法
1.如图②,在边 上取一点 ,过点 作 交 于点 .
2.以点 为圆心, 长为半径画弧,交 于点 .
3.在 上截取 ,连接 ,则四边形 为所求作的菱形.
(1)证明小明所作的四边形 是菱形.
(2)小明进一步探索,发现可作出的菱形的个数随着点 的位置变化而变化 请你继续探索,直接写出菱形的个数及对应的 的长的取值范围.