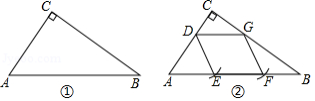
如图①,在 中, , , .求作菱形 ,使点 在边 上,点 、 在边 上,点 在边 上.
小明的作法
1.如图②,在边 上取一点 ,过点 作 交 于点 .
2.以点 为圆心, 长为半径画弧,交 于点 .
3.在 上截取 ,连接 ,则四边形 为所求作的菱形.
(1)证明小明所作的四边形 是菱形.
(2)小明进一步探索,发现可作出的菱形的个数随着点 的位置变化而变化 请你继续探索,直接写出菱形的个数及对应的 的长的取值范围.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

(1)计算: .
(2)解不等式组 .
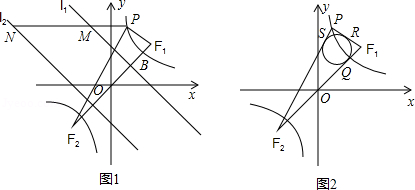
如图1所示,已知:点A(﹣2,﹣1)在双曲线 上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1,l2于M,N两点.
(1)求双曲线C及直线l2的解析式;
(2)求证: ;
(3)如图2所示,△PF1F2的内切圆与F1F2,PF1,PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1,y1),B(x2,y2),则A、B两点间的距离公式为 .
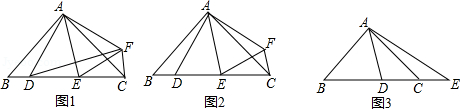
在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
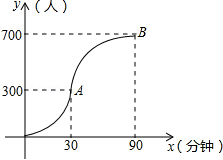
科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为 ,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?