某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品 (吨),生产甲、乙两种产品获得的总利润为 (万元).
(1)求 与 之间的函数表达式;
(2)若每生产1吨甲产品需要 原料0.25吨,每生产1吨乙产品需要 原料0.5吨.受市场影响,该厂能获得的 原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
计算:
(1) ;
;
(2) .
.
如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
(1)求出绿地的面积;(用含a、b的代数式表示)
(2)若a=2b,且道路的面积为224米2,求原长方形空地的宽.
计算:(3x2y)•(﹣2xy)﹣(﹣2x2y3)2÷(﹣4xy4).
计算题:
(1)(﹣2009)0﹣2﹣2+( )2
)2 ;
;
(2)(9x3y2﹣6x2y+3xy2)÷(﹣3xy);
(3)(a﹣2)2﹣(2a﹣1)(a+4);
(4)用乘法公式计算:(x﹣2y+3)(x+2y﹣3).
计算:
(1)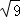 +|
+| |﹣(x﹣1)0
|﹣(x﹣1)0
(2)(6x3﹣12x2+3x)÷3x.