如图所示为“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成的,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连接而成的,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球从a点水平射向b点并进入轨道,经过轨道后从p点水平抛出,已知小球与地面ab段间的动摩擦因数μ=0.2,不计其他机械能损失,ab段长L=1.25 m,圆的半径R=0.2 m,小球质量m=0.01 kg,轨道质量为
M=0.425 kg,g=10 m/s2,求:
(1)若v0=5 m/s,小球从p点抛出后的水平射程;
(2)若v0=5 m/s,小球经过轨道的最高点时,管道对小球作用力的大小和方向;
(3)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v0至少为多大时,轨道对地面的压力可以为零.
冬季有一种雪上“府式冰撬”滑溜运动,运动员从起跑线推着冰撬加速一段相同距离,再跳上冰撬自由滑行,滑行距离最远者获胜,运动过程可简化为如图所示的模型,某一质量m=20kg的冰撬静止在水平雪面上的A处,现质量M=60kg的运动员,用与水平方向成α=37°角的恒力F=200N斜向下推动冰撬,使其沿AP方向一起做直线运动,当冰撬到达P点时运动员迅速跳上冰撬与冰撬一起运动(运动员跳上冰撬瞬间,运动员和冰撬的速度不变).已知冰撬从A到P的运动时间为2s,冰撬与雪面间的动摩擦因数为0.2,不计冰撬长度和空气阻力.(g取10m/s2,cos 37°=0.8)求: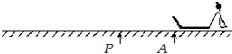
(1)AP的距离;
(2)冰撬从P点开始还能继续滑行多久?
如图所示,一质量为m的氢气球用细绳拴在地面上,地面上空风速水平且恒为v0,球静止时绳与水平方向夹角为α.已知风力的大小与风速成正比,可以表示为f=kv(k为已知的常数).求: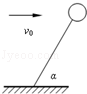
(1)氢气球受到的浮力为多大;
(2)某时刻绳突然断裂,则绳断裂瞬间氢气球加速度为多大?
如图,一个人站在水平地面上的长木板上用力F向右推箱子,木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g,则()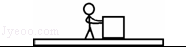
| A.箱子受到的摩擦力方向向右 |
| B.地面对木板的摩擦力为零 |
| C.木板对地面的压力大小为3mg |
| D.若人用斜向下的力推箱子,则木板对地面的压力仍然为3mg |
如图,A、B、C三个木块的质量均为m,置于光滑的水平桌面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连.将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体.现A以初速度v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起.以后细线突然断开,弹簧伸展,从而使C与A、B分离.已知离开弹簧后C的速度恰好为v0.求弹簧释放的势能.
一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面,赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m处下潜到深度为h2=4.0m时,看到标记刚好被浮标挡住,此处看不到船尾端Q,继续下潜△h=4.0m,恰好能看见Q.求:
(1)水的折射率n;
(2)赛艇的长度1.(可用根式表示)