如图所示,MN是一条通过透明球体球心的直线,一条平行于MN的光线a射向此球体,若出射光线c与MN的交点P和球心O的距离是球半径的 倍,与MN所成的角α=30°,求(1)完成光路图(2)透明球体的折射率.
倍,与MN所成的角α=30°,求(1)完成光路图(2)透明球体的折射率.
如图所示,质量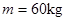 的高山滑雪运动员,从
的高山滑雪运动员,从 点由静止开始沿滑道自由滑下,到
点由静止开始沿滑道自由滑下,到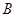 点时沿与水平方向成
点时沿与水平方向成 角斜向上飞出,最后落在斜坡上的
角斜向上飞出,最后落在斜坡上的 点。已知
点。已知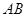 两点间的高度差为
两点间的高度差为 ,
,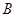 、
、 两点间的高度差为
两点间的高度差为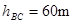 ,运动员从
,运动员从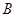 点飞出时的速度为20m/s(
点飞出时的速度为20m/s(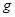 取10m/s2)求:(1)运动员从
取10m/s2)求:(1)运动员从 到
到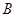 克服摩擦阻力做的功;(2)运动员落到C点时的速度大小。
克服摩擦阻力做的功;(2)运动员落到C点时的速度大小。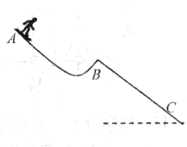
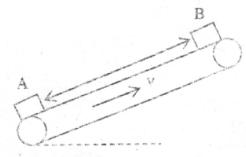
如图所示,传送带与水平面之间的夹角为37°,其上A、B两点间的距离为5.6m,传送带在电动机的带动下以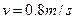 的速度匀速运转,现将一质量为
的速度匀速运转,现将一质量为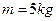 的小物体(可视为质点)轻放在传送带上A点,已知小物体从A到B的时间一共为8s,则在传送带将小物块从A传送到B的过程中,求:
的小物体(可视为质点)轻放在传送带上A点,已知小物体从A到B的时间一共为8s,则在传送带将小物块从A传送到B的过程中,求:小物块与传送带之间的动摩擦因数为多少?
小物块对传送带的摩擦力对传送带做了多少功?
若每隔
 轻放一个同样的物体,当物体稳定运行时,相邻匀速运动的两物体之间的距离为多大?
轻放一个同样的物体,当物体稳定运行时,相邻匀速运动的两物体之间的距离为多大?若每隔
 轻放一个同样的物体,不计传送带与轮轴处的摩擦损耗,求带动传送带的电动机在相当长一段时间内的平均输出功率为多大?(
轻放一个同样的物体,不计传送带与轮轴处的摩擦损耗,求带动传送带的电动机在相当长一段时间内的平均输出功率为多大?(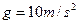 )
)
如图所示,光滑水平面上有一质量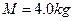 的带有圆弧轨道的平板车,车的上表面是一段长
的带有圆弧轨道的平板车,车的上表面是一段长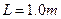 的粗糙水平轨道,水平轨道左侧连一半径
的粗糙水平轨道,水平轨道左侧连一半径 的
的 光滑圆弧轨道,圆弧轨道与水平轨道在O′点相切,车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧,一质量
光滑圆弧轨道,圆弧轨道与水平轨道在O′点相切,车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧,一质量 的小物块紧靠弹簧放置,小物块与水平轨道间的动摩擦因数
的小物块紧靠弹簧放置,小物块与水平轨道间的动摩擦因数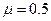 ,整个装置处于静止状态,现将弹簧解除锁定,小物块被弹出,恰能到达圆弧轨道的最高点A,取
,整个装置处于静止状态,现将弹簧解除锁定,小物块被弹出,恰能到达圆弧轨道的最高点A,取 ,求:
,求: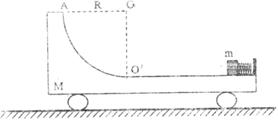
小物块到达A点时,平板车的速度大小;
解除锁定前弹簧的弹性势能;
小物块第二次经过O′点时的速度大小;
小物块与车最终相对静止时,它距O′点的距离。
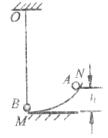
如图所示,A,B为两个大小可视为质点的小球,A的质量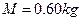 ,B的质量
,B的质量 ,B球用长
,B球用长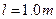 的轻质细绳吊起,当细绳位于竖直位置,B球处于静止状态时,B球恰好与弧形轨道MN的末端接触但无作用力,已知弧形轨道的内表面光滑,且末端切线水平,现使A球从距轨道末端
的轻质细绳吊起,当细绳位于竖直位置,B球处于静止状态时,B球恰好与弧形轨道MN的末端接触但无作用力,已知弧形轨道的内表面光滑,且末端切线水平,现使A球从距轨道末端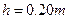 的高处由静止释放,当A球运动到轨道末端时与B球发生完全弹性碰撞。若
的高处由静止释放,当A球运动到轨道末端时与B球发生完全弹性碰撞。若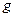 取
取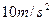 ,求:
,求:A球刚要接触到B球时的速度大小;
两小球相碰撞过程中,B球对A球所做的功;
两个小球碰撞后各自开始运动的瞬间,B球对细绳的拉力大小。
一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道绕行数圈后,着陆在该行星上。飞船上备有以下实验器材:①精确秒表一只;②已知质量为 的物体一个;③弹簧测力计一个。若宇航员在绕行时测出了飞船绕行星运行的周期为T,着陆后质量为
的物体一个;③弹簧测力计一个。若宇航员在绕行时测出了飞船绕行星运行的周期为T,着陆后质量为 的物体所受重力为F。并已知万有引力常量为G,行星的自转可忽略不计,试求出该星球的半径R及星球的质量M。
的物体所受重力为F。并已知万有引力常量为G,行星的自转可忽略不计,试求出该星球的半径R及星球的质量M。