若函数f(x)=sin2ax-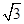 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈ ,求点A的坐标.
,求点A的坐标.
.(本小题满分12分)
一个盒子里装有4张卡片,分别标有数2,3,4,5;另一个盒子里则装有分别标有3,4,5,6四个数的4张卡片.从两个盒子里各任取一张卡片.
(1)求取出的两张卡片上的数不同的概率;
(2)求取出的两张卡片上的数之和ξ的期望.
(本小题满分12分)
已知△ABC中,a,b,c分别是角A,B,C的对边,A是锐角,且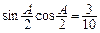 ,
,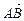 ·
·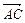 =8.
=8.
(1)求bc的值;
(2)求a的最小值.
(本小题满分14分)
已知函数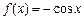 ,
,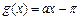 .
.
(1)若函数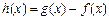 在
在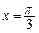 时取得极值,求
时取得极值,求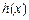 的单调递减区间;
的单调递减区间;
(2)证明:对任意的x∈R,都有|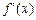 |≤| x |;
|≤| x |;
(3)若a=2,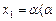 ∈[
∈[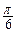 ,
, ]),
]),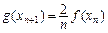 ,求证:
,求证: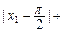
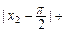 …+
…+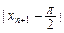 <
<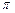 (n∈N*).
(n∈N*).
(本小题满分13分)
已知过椭圆C: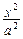 +
+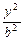 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数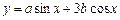 图象的一条对称轴的方程是
图象的一条对称轴的方程是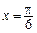 .
.
(1)求椭圆 C
C 的离心率e与直线AB的方程;
的离心率e与直线AB的方程;
(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式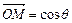
 +
+
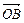 成立.
成立.
(本小题满分12分)
已知函数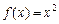 ,
,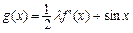 在[-1,1]上是减函数
在[-1,1]上是减函数 .
.
(1)求曲线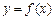 在点(1,
在点(1,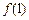 )处的切线方程;
)处的切线方程;
(2)若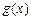 ≤
≤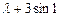 在x∈[-1,1]上恒成立,求
在x∈[-1,1]上恒成立,求 的取值范围;
的取值范围;