数学课上,李老师出示了这样一道题目:如图,正方形 的边长为
的边长为 ,
, 为边
为边 延长线上的一点,
延长线上的一点,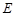 为
为 的中点,
的中点, 的垂直平分线交边
的垂直平分线交边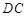 于
于 ,交边
,交边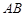 的延长线于
的延长线于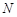 .当
.当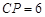 时,
时, 与
与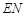 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过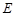 作直线平行于
作直线平行于 交
交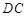 ,
,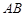 分别于
分别于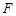 ,
,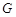 ,如图
,如图 ,则可得:
,则可得: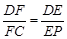 ,因为
,因为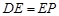 ,所以
,所以 .可求出
.可求出 和
和 的值,进而可求得
的值,进而可求得 与
与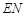 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了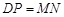 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”。
若A、B的坐标分别是(1,0)和(0,2).在下图的网格中找出符合条件的“整点P”。
(1)若△APB是等腰三角形,满足条件的整点P共有个.它们的坐标分别是;
(2)若△APB是直角三角形,满足条件的整点P共有个.它们的坐标分别是。
已知: ,求
,求 的值。
的值。
计算:| -3|+(π-1)0-
-3|+(π-1)0- +
+
某旅游景点的门票价格规定如下表所示:
| 团体购票人数 |
1~50人 |
51~100人 |
100人以上 |
| 每人门票价(团体价) |
13元 |
11元 |
a元 |
学校七年级(1)(2)两个班共104人去旅游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,经估算,如果两个班都以班为单位分别购票,一共应付款1240元.
(1)问两班各有学生多少名?
(2)如果两个班联合起来,作为一个团体购票,可节省304元,试求a的值.
(3)某学校七年级有12个班,每班45人,若该校七年级各班统一组织来到此景点春游,问:全年级作为一个团体购票比各班单独购票能节省多少费用?
如图,直线AC∥BD,连结AB,直线AC、BD把之间的平面分成①、②两个部分,规定线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB构成∠PAC、∠APB、∠PBD三个角.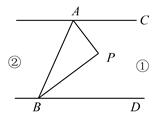
(1)当动点P落在第①部分时,试说明:∠APB=∠PAC+∠PBD;(提示:过点P作直线与AC平行)
(2)当动点P落在第②部分时,请画出相应的图形.试探究∠APB、∠PAC、∠PBD之间的数量关系,并说明理由.