某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为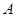 饮料,另外4杯为
饮料,另外4杯为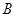 饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯
饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯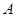 饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令
饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令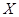 表示此人选对
表示此人选对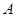 饮料的杯数.假设此人对
饮料的杯数.假设此人对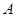 和
和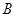 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(1)求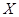 的分布列;
的分布列;
(2)求此员工月工资被定为2100元的概率.
(本小题满分12分)
如图:A、B两城相距100 km,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气. 已知D地距A城x km,为保证城市安全,天燃气站距两城市的距离均不得少于10km . 已知建设费用y (万元)与A、B两地的供气距离(km)的平方和成正比,当天燃气站D距A城的距离为40km时, 建设费用为1300万元.(供气距离指天燃气站距到城市的距离)
(1)把建设费用y(万元)表示成供气距离x (km)的函数,并求定义域;
(2)天燃气供气站建在距A城多远,才能使建设供气费用最小.,最小费用是多少?
(本小题满分14分)
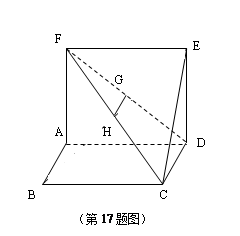
如图,正方形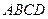 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面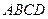 互相垂直,
互相垂直,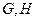 是
是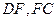 的中点.
的中点.
(1)求证: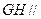 平面
平面 ;
;
(2)求证: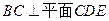 ;
;
(3)求三棱锥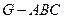 的体积.
的体积.
(本小题满分14分)
求经过直线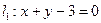 与直线
与直线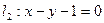 的交点M,且分别满足下列条件的直线方程:
的交点M,且分别满足下列条件的直线方程:
(1)与直线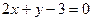 平行;
平行;
(2)与直线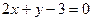 垂直.
垂直.
(本小题满分12分)
已知集合 ,集合
,集合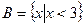 .
.
(1)求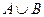 ;
;
(2)求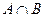 ;
;
(3)求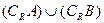
已知函数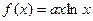 图像上点
图像上点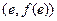 处的切线与直线
处的切线与直线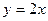
平行(其中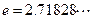 ),
),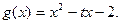 (I)求函数
(I)求函数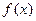 的解析式;
的解析式;
(II)求函数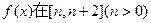 上的最小值;
上的最小值;
(III)对一切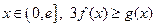 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。