某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
(1) 试分别估计两个分厂生产的零件的优质品率;
(2) 由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| |
甲 厂 |
乙 厂 |
合计 |
| 优质品 |
|
|
|
| 非优质品 |
|
|
|
| 合计 |
|
|
|
附: ,
,

 .
.
(本小题满分13分)
某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资m万元(m为正常数).
(Ⅰ)以2009年为第一年,求第n年底该县农村医保基金有多少万元?
(Ⅱ)根据该县农村人口数量和财政状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金m(单位:万元)应控制在什么范围内.
(本小题满分12分)
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
(Ⅰ)求二面角M-AC-B大小的正切值;
(Ⅱ)求三棱锥P-MAC的体积.
 |
(本小题满分12分)
湖南省有许多旅游景点,某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点,并收藏有张家界纪念门票3张,南岳纪念门票2张,韶山、岳阳楼、桃花源纪念门票各1张,现从中随机抽取5张.
(Ⅰ)求抽取的5张门票中恰有3个或恰有4个景点的概率;
(Ⅱ)若抽取的5张门票中5个景点都有记10分,恰有4个景点记8分,恰有3个景点记6分,依此类推.设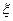 表示所得的分数,求
表示所得的分数,求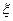 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
设△ABC的三内角A、B、C的对边长分别为a、b、c,已知a、b、c成等比数列,且 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若 ,求函数
,求函数 的值域.
的值域.
已知函数
(
,
)为偶函数,
且函数
图象的两相邻对称轴间的距离为
.
⑴求
的值;
⑵将函数
的图象向右平移
个单位后,得到函数
的图象,求
的单调递减区间.