关于
的方程
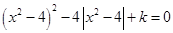，给出下列四个命题：
①存在实数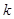
，使得方程恰有2个不同的实根；
②存在实数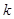，使得方程恰有4个不同的实根；
③存在实数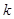，使得方程恰有5个不同的实根；
④存在实数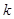，使得方程恰有8个不同的实根.
其中假命题的个数是
| A．0 | B．1 | C．2 | D．3 |
函数
的定义域为（）
| A．[1，2)∪(2，+∞） | B．(1，+∞） | C．[1， 2) | D．[2，+∞) |
设集合A=｛2,3｝，B=｛3,4｝,C=｛3,4,5｝则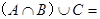
（）
| A．｛2,3,4｝ | B．｛2,3,5｝ | C．｛3,4,5｝ | D．｛2,3,4,5｝ |
下列说法中：
① 若
（其中
）是偶函数，则实数
；
② 
既是奇函数又是偶函数；
③ 函数
的减区间是
；
④ 已知
是定义在
上的不恒为零的函数，且对任意的
都满足
，则是奇函数。
其中正确说法的序号是( )
| A．①②④ | B．①③④ |
| C．②③④ | D．①②③ |
函数f（x）=4x－3·2x＋3的值域为[1，7]，则f（x）的定义域为（）
| A．（－1，1）∪[2，4] ( | B．（0，1）∪[2，4] |
| C． [2，4] | D．（－∞，0] ∪[1，2] |
设集合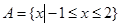
,
,
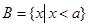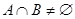,则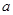
的取值范围是（）
A． |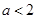
B． |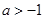
C． ( |
D． |