数学兴趣小组到外旅游拍一张合影,冲一张底片需1.6元,洗一张照片需0.55元。若每人都得到一张照片,那么平均每人分摊的钱不超过0.7元,问这个小组至少有多少人?
下表是某班20名学生的一次语文测验的成绩分布表:
| 成绩 |
50 |
60 |
70 |
80 |
90 |
| 人数(人) |
2 |
3 |
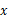 |
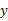 |
2 |
根据上表,若成绩的平均数是72,计算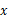 ,
,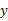 的值.
的值.
小颖家去年的饮食支出3 600元,教育支出1 200元,其他支出7 200元,小颖家今年的这三项支出依次比去年增长了9%,30%,6%,请你帮小颖算一算今年的总支出比去年增长的百分数是多少?
小明是这样帮她算的: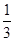
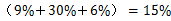 .
.
你认为他这样计算对吗?为什么?
小洁在某超市购买了3盒1升装的牛奶,每盒5.80元,另外又买了12盒250毫升装的牛奶,每盒1.50元,那么她平均每盒花费了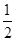
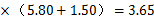 元,对吗?如果不对的话,请给出正确的结果.
元,对吗?如果不对的话,请给出正确的结果.
为调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了8名学生,他们每天完成作业所需时间(单位: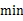 )分别为:60,55,75,55,55,43,65,40.
)分别为:60,55,75,55,55,43,65,40.
(1)求这组数据的众数、中位数.
(2)求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过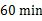 ,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?
,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?
观察下表:
| 列举 |
猜想 |
| 3,4,5 |
 |
| 5,12, 13 |
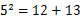 |
| 7,24,25 |
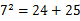 |
| … … … |
… … … |
 |
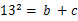 |
请你结合该表格及相关知识,求出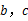 的值.
的值.