抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值并在图中画出这条抛物线.
(2)求它与x轴的交点和抛物线顶点的坐标.
(3)x取值什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x的增大而减小?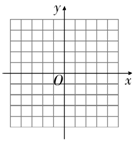
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,BP=3 (单位:km)有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(单位:km)有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.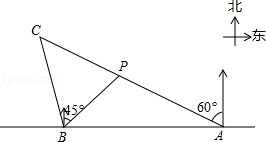
(1)求A、B两个观测站之间的距离;
(2)小船从点P处沿射线AP的方向以 千米/时的速度进行沿途考查,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°的方向,求小船沿途考察的时间.(结果有根号的保留根号)
千米/时的速度进行沿途考查,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°的方向,求小船沿途考察的时间.(结果有根号的保留根号)
某大学举办教工男子篮球赛,由大学各个院系教工组成A、B、C、D、E五个代表队,由大学附属单位组成F、G、H三个代表队.通过抽签分组,比赛共分上下两个半区,上半区有A、D、E、G四个代表队,下半区有B、C、F、H四个代表队.若从上下半区各随机抽取一个代表队进行首场比赛,请列表或画树状图写出所有可能的结果,并计算首场比赛的两个代表队都是大学附属单位代表队的概率.
如图,已知△ABC,用尺规作出△ABC的一条中位线.(保留作图痕迹,不写作法)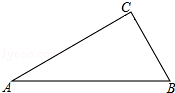
用适当的方法解方程.
(1)4x2-x-1=3x-2
(2)2y2+7y-3=0.
(12分) 已知⊙O的半径为2,∠AOB=120°。
(1)点O到弦AB的距离为 .
(2)若点P为优弧AB上一动点(点P不与A、B重合),设∠ABP=α,将△ABP沿BP折叠,得到A点的对称点为A';
①若∠α=30°,试判断点A'与⊙O的位置关系;
②若BA'与⊙O相切于B点,求BP的长;
③若线段BA'与优弧APB只有一个公共点,直接写出α的取值范围.