如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点, PO的延长线交BC于Q.
(1)求证:△ P O D ≌ △Q O B ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形P B Q D是菱形.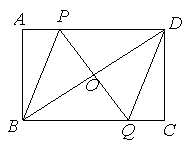
解下列二元一次方程组
(1)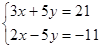 (2)
(2)
如图,直线 和x轴、y轴的交点分别为B、C,点A的坐标是(
和x轴、y轴的交点分别为B、C,点A的坐标是( ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
(1)求直线AC所对应的函数表达式;
(2)动点M从B出发沿BC运动,运动的速度为每秒1个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.
① 求S与t的函数关系式;
② 当t为何值时, (注:
(注: 表示△ABC的面积),求出对应的t值;
表示△ABC的面积),求出对应的t值;
③当 t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由。
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,下图是甲、乙两车间的距离 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像.
(时)的函数的部分图像.
(1)A、B两地的距离是千米,乙车出发小时与甲相遇;
(2)求乙车出发1.5小时后直至到达A地的过程中, 与
与 的函数关系式及
的函数关系式及 的取值范围;
的取值范围;
(3)乙车出发多长时间,两车相距100千米?
为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买x个文具盒,10件奖品共需w元,求w与x的函数关系式。如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
如图,△ABD、△CBD都是等边三角形,DE、BF分别是△ABD的两条高,DE、BF交于点G.
(1)求∠BGD的度数
(2)连接CG
①求证:BG+DG=CG
②求 的值
的值