(本题12分)
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如: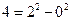 ,
,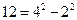 ,
,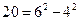 ,因此
,因此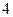 ,
,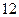 ,
,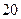 这三个数都是神秘数.
这三个数都是神秘数.
(1)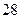 和
和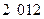 这两个数是神秘数吗?为什么?
这两个数是神秘数吗?为什么?
(2)设两个连续偶数为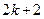 和
和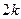 (其中
(其中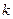 取非负整数),由这两个连续偶数构造的神秘数是
取非负整数),由这两个连续偶数构造的神秘数是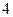 的倍数吗?为什么?
的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
(1)计算: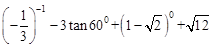 ;
;
(2)先化简,再求代数式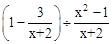 的值,其中x是不等式组
的值,其中x是不等式组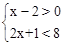 的整数解.
的整数解.
如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.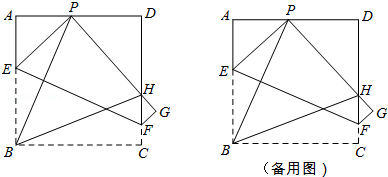
现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
| 运往甲地(单位:吨) |
运往乙地(单位:吨) |
|
| A |
x |
|
| B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G.
(1)判断直线AG与⊙O的位置关系,并说明理由.
(2)求线段AF的长.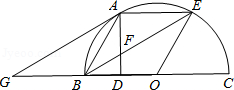
若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从1,2,3,4这四个数字中任取3个数,组成无重复数字的三位数.
(1)请画出树状图并写出所有可能得到的三位数;
(2)甲、乙二人玩一个游戏,游戏规则是:若组成的三位数是“伞数”,则甲胜;否则乙胜.你认为这个游戏公平吗?试说明理由.