阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用___________法达到________的目的,体现了
数学的转化思想.
(2)解方程(x2+x)2-4(x2+x)-12=0.
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,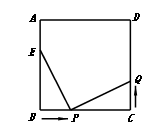
①CP的长为 cm(用含t的代数式表示);
②若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
③若点Q的运动速度与点P的运动速度不相等,△BPE与△CQP能否全等,若能全等,求出点Q的运动速度,若不能全等,请说明理由.
两个大小不同的等腰直角三角形三角板按图1所示的位置放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.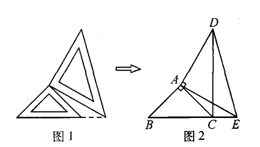
(1)请找出图2中与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,使整个图形(包括空白方格)是一个轴对称图形,至少画出四种.
如图所示,两根旗杆间相距12 m,某人从B点沿BA走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为5 m,该人的运动速度为1 m/s,求这个人运动了多长时间?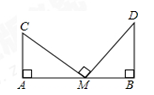
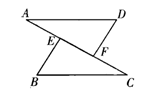
如图,已知点A、E、F、C在同一直线上,AD∥BC,AD=BC,AE=CF,求证:DF∥BE.