如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,
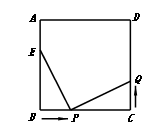
①CP的长为 cm(用含t的代数式表示);
②若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
③若点Q的运动速度与点P的运动速度不相等,△BPE与△CQP能否全等,若能全等,求出点Q的运动速度,若不能全等,请说明理由.
如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 .
(1)求证: 为 的切线;
(2)若 ,求弧 的长.

为了积极响应中共中央文明办关于"文明用餐"的倡议,某校开展了"你的家庭使用公筷了吗?"的调查活动,并随机抽取了部分学生,对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种: (完全使用)、 (多数时间使用)、 (偶尔使用)、 (完全不使用),将数据进行整理后,绘制了两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)本次抽取的学生总人数共有 ;
(2)补全条形统计图;
(3)扇形统计图中 对应的扇形的圆心角度数是 ;
(4)为了了解少数学生完全不使用公筷的原因,学校决定从 组的学生中随机抽取两位进行回访,若 组中有3名男生,其余均为女生,请用列表法或画树状图的方法,求抽取的两位学生恰好是一男一女的概率.
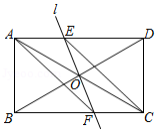
如图,在矩形 中,对角线 与 相交于点 , ,对角线 所在的直线绕点 顺时针旋转角 ,所得的直线 分别交 , 于点 , .
(1)求证: ;
(2)当旋转角 为多少度时,四边形 为菱形?试说明理由.
2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
先化简 ,然后从0,1,2,3中选一个合适的 值代入求解.