）某商场服装部销售一种名牌衬衫，平均每天可售出30件，每件盈利40元．为了扩大销售，减少库存，商场决定降价销售，经调查，每件降价1元时，平均每天可多卖出2件．
（1）若商场要求该服装部每天盈利1200元，每件衬衫应降价多少元？
（2）试说明每件衬衫降价多少元时，商场服装部每天盈利最多．
设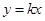
，是否存在实数
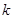，使得代数式
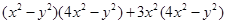能化简为
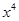？若能，请求出所有满足条件的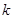值，若不能，请说明理由.
在
中，
，点
,
分别在
,
上，
，
与
相交于点
，求证：
，并请直接写出图中其他相等的线段.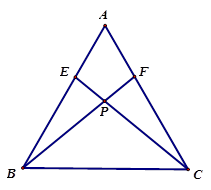
一个布袋中装有只有颜色不同的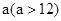
个球，分别是2个白球，4个黑球，6个红球和b个黄球，从中任意摸出一个球，把摸出白球，黑球，红球的概率绘制成统计图（未绘制完整），请补全该统计图并求出
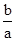的值.
如图，抛物线y=x²+bx+c与直线y=x－1交于A、B两点.点A的横坐标为－3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D.
（1）求抛物线的解析式；
（2）当m为何值时，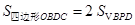
；
（3）是否存在点P,使△PAD是直角三角形，若存在，求出点P的坐标；若不存在，说明理由.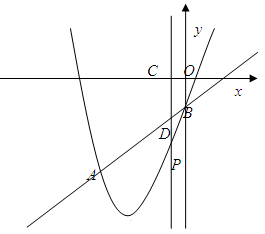
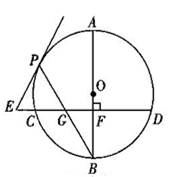
如图，已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG,
（1）求证：直线EP为⊙O的切线；
（2）点P在劣弧AC上运动，其他条件不变，若BG²=BF·BO.试证明BG=PG.
（3）在满足（2）的条件下，已知⊙O的半径为3，sinB=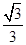
.求弦CD的长.