.(本小题满分12分)在一次数学考试中,第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做这两题的可能性均为 .
.
(Ⅰ)求其中甲、乙二名学生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为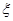 ,求
,求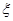 的概率分布及数学期望.
的概率分布及数学期望.
已知椭圆的中点在原点且过点 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
设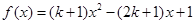 ,
,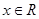 .
.
(1)若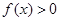 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)若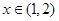 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当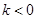 时,解不等式
时,解不等式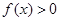 .
.
已知集合M={1,2,3,4,5}, .
.
(1)用列举法表示集合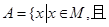
 ;
;
(2)设N是M的非空真子集,且 时,有
时,有 ,试写出所有集合N;
,试写出所有集合N;
(3)已知M的非空子集个数为31个,依次记为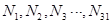 ,分别求出它们各自的元素之和,结果依次记为
,分别求出它们各自的元素之和,结果依次记为 ,试计算:
,试计算: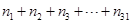 的值.
的值.
已知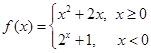 .
.
(1)已知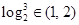 ,分别求
,分别求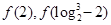 的值;
的值;
(2)画出函数 的图像,并指出函数的单调区间(不要求证明);
的图像,并指出函数的单调区间(不要求证明);
(3)解不等式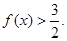

将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时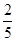 小时,种植一捆沙棘用时
小时,种植一捆沙棘用时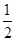 小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨仍用时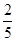 小时,而每名志愿者种植一捆沙棘实际用时
小时,而每名志愿者种植一捆沙棘实际用时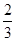 小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.