如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?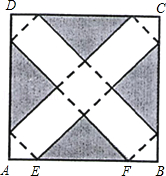
(成都)(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
(凉山州)阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF=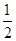 (AD+BC)
(AD+BC)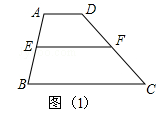
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点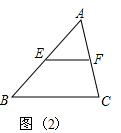
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD=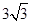 ,OC=5,求MN的长.
,OC=5,求MN的长.
(遂宁)阅读下列材料,并用相关的思想方法解决问题.
计算: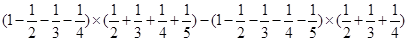 .
.
令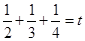 ,则
,则
原式=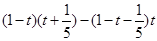
=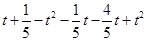
=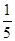
问题:(1)计算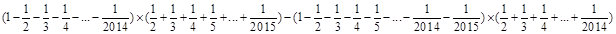 ;
;
(2)解方程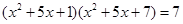 .
.
(自贡)观察下表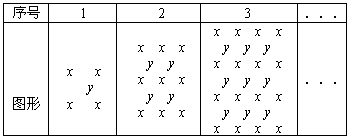
我们把某格中字母和所得的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,
①求x,y的值;
②在此条件下,第n格的特征是否有最小值?若有,求出最小值和相应的n值,若没有,说明理由.
(达州)阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为 ,所以
,所以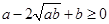 从而
从而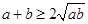 (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数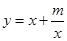 ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知: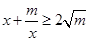 ,所以当
,所以当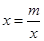 ,即
,即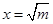 时,函数
时,函数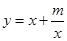 的最小值为
的最小值为 .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为2(
,周长为2( ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数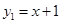 (
(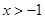 )与函数
)与函数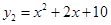 (
(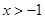 ),
),
当x= 时,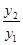 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)