已知:抛物线 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
(1)求该抛物线的表达式和点B的坐标;
(2)设C为该抛物线的顶点,⊙C的半径长为2.以该抛物线对称轴上一点P为圆心,线段PO的长为半径作⊙P,如果⊙P与⊙C相切,求点P的坐标.
已知:如图, 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是 外一点,PA切
外一点,PA切 于点A,且PA=PB.
于点A,且PA=PB.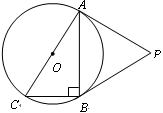
(1)求证:PB是 的切线;
的切线;
(2)已知PA= ,BC=2,求
,BC=2,求 的半径.
的半径.
已知:如图,四边形 中,对角线AC、BD相交于点E,
中,对角线AC、BD相交于点E, ,
, ,
, . 求对角线
. 求对角线 的长和
的长和 的面积.
的面积.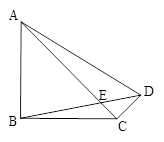
如图,在平面直角坐标系 中,一次函数
中,一次函数 的图象与
的图象与 轴相交于点
轴相交于点 ,与
,与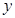 轴相交于点
轴相交于点 ,与反比例函数图象相交于点
,与反比例函数图象相交于点 ,且
,且 .
.
(1)求反比例函数的解析式;
(2)若点 在
在 轴上,且
轴上,且 的面积等于12,直接写出点
的面积等于12,直接写出点 的坐标.
的坐标.
列方程或方程组解应用题:
某企业向四川雅安地震灾区捐助价值17.6万元的甲、乙两种帐篷共200顶,已知甲种帐篷每顶800元,乙种帐篷每顶1000元,问甲、乙两种帐篷各多少顶?
已知:如图,在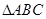 中,
中,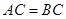 ,
,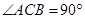 ,
,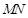 是过点
是过点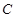 的一条直线,
的一条直线, 于
于 ,
,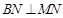 于
于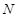 ,求证:
,求证:  .
.